
【題目】如圖,正方形ABCD內部有若干個點,用這些點以及正方形ABCD的頂點A,B,C,D把原正方形分割成一些三角形(互相不重疊):

(1)填寫下表:

(2)原正方形能否被分割成2018個三角形?若能,求此時正方形ABCD內部有多少個點;若不能,請說明理由.
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上有三個點A,B,C,回答下列問題:
(1)若將點B向右移動6個單位后,三個點所表示的數中最小的數是多少?
(2)在數軸上找一點D,使點D到A,C兩點的距離相等,寫出點D表示的數;
(3)在點B左側找一點E,使點E到點A的距離是到點B的距離的2倍,并寫出點E表示的數.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+c(b>a>0)與x軸最多有一個交點,現有以下四個結論:
①該拋物線的對稱軸在y軸左側;
②關于x的方程ax2+bx+c+2=0無實數根;
③a﹣b+c≥0;
④ ![]() 的最小值為3.
的最小值為3.
其中,正確結論的個數為( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩站相距240千米,從甲站開出一列慢車,速度為每小時80千米,從乙站開出一列快車,速度為每小時120千米.
(1)若兩車同時開出,背向而行,則經過多長時間兩車相距540千米?
(2)若兩車同時開出,同向而行(快車在后),則經過多長時間快車可追上慢車?
(3)若兩車同時開出,同向而行(慢車在后),則經過多長時間兩車相距300千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若一個正整數能表示為兩個正整數的平方差,則稱這個正整數為“智慧數”(如3=22-12,16=52-32,則3和16是智慧數).已知按從小到大的順序構成如下數列:3,5,7,8,9,11,12,13,15,16,17,19,20,21,23,24,25,…則第2 013個“智慧數”是______.
【答案】2 687
【解析】解析:觀察數的變化規律,可知全部“智慧數”從小到大可按每三個數分一組,從第2組開始每組的第一個數都是4的倍數,歸納可得,第n組的第一個數為4n(n≥2).因為2 013÷3=671,所以第2 013個“智慧數”是第671組中的第3個數,即為4×671+3=2 687.
點睛:找規律題需要記憶常見數列
1,2,3,4……n
1,3,5,7……2n-1
2,4,6,8……2n
2,4,8,16,32……![]()
1,4,9,16,25……![]()
2,6,12,20……n(n+1)
一般題目中的數列是利用常見數列變形而來,其中后一項比前一項多一個常數,是等差數列,列舉找規律.后一項是前一項的固定倍數,則是等比數列,列舉找規律.
【題型】填空題
【結束】
19
【題目】如圖,鄭某把一塊邊長為a m的正方形的土地租給李某種植,他對李某說:“我把你這塊地的一邊減少5 m,另一邊增加5 m,繼續租給你,你也沒有吃虧,你看如何”.李某一聽,覺得自己好像沒有吃虧,就答應了.同學們,你們覺得李某有沒有吃虧?請說明理由.
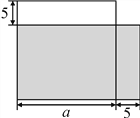
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有5張看上去無差別的卡片,上面分別寫著1,2,3,4,5,隨機抽取3張,用抽到的三個數字作為邊長,恰能構成三角形的概率是( )
A.![]() ?
?
B.![]() ?
?
C.![]() ?
?
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
【答案】(1)-195(2)2xy-2
【解析】試題分析:(1)利用平方差公式,完全平方公式簡便計算.
(2)提取公因式,化簡.
試題解析:
(1)原式=(100-1)2-(100+2)×(100-2)
=(1002-200+1)-(1002-4)=-200+5=-195.
(2)原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y=2(xy-1)=2xy-2.
【題型】解答題
【結束】
21
【題目】(1)先化簡,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與x軸交于A、B兩點,與y軸交于點C(0,3),且此拋物線的頂點坐標為M(﹣1,4).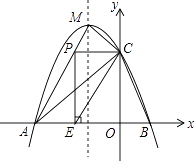
(1)求此拋物線的解析式;
(2)設點D為已知拋物線對稱軸上的任意一點,當△ACD與△ACB面積相等時,求點D的坐標;
(3)點P在線段AM上,當PC與y軸垂直時,過點P作x軸的垂線,垂足為E,將△PCE沿直線CE翻折,使點P的對應點P′與P、E、C處在同一平面內,請求出點P′坐標,并判斷點P′是否在該拋物線上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某生物興趣小組在四天的實驗研究中發現:駱駝的體溫會隨外部環境溫度的變化而變化,而且在這四天中每晝夜的體溫變化情況相同.他們將一頭駱駝前兩晝夜的體溫變化情況繪制成下圖.請根據圖像回答問題:
(1)第一天中,在什么時間范圍內這頭駱駝的體溫是上升的?它的體溫從最低上升到最高需要多少時間?
(2)第三天12時這頭駱駝的體溫約是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com