Question

【題目】“校園安全”受到全社會的廣泛關注，東營市某中學對部分學生就校園安全知識的了解程度，采用隨機抽樣調查的方式，并根據收集到的信息進行統(tǒng)計，繪制了下面兩幅尚不完整的統(tǒng)計圖．請你根據統(tǒng)計圖中所提供的信息解答下列問題：

（1）接受問卷調查的學生共有_______人，扇形統(tǒng)計圖中“基本了解”部分所對應扇形的圓心角為_______°；

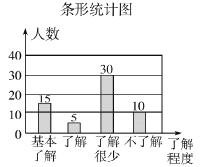
（2）請補全條形統(tǒng)計圖；

（3）若該中學共有學生900人，請根據上述調查結果，估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數；

（4）若從對校園安全知識達到“了解”程度的3個女生和2個男生中隨機抽取2人參加校園安全知識競賽，請用樹狀圖或列表法求出恰好抽到1個男生和1個女生的概率．

Answer 1

【答案】（1）60,90°；（2）詳見解析；（3）300；（4）.

【解析】

試題分析：（1）在扇形圖中找到“了解很少”所占的百分比，在條形圖中找出“了解很少”所對應的人數，據此即可求出接受問卷調查的學生總人數；在條形圖中找出“基本了解”部分的人數，用這個人數除以接受調查的總人數所得的商再乘以360°，即可求出扇形統(tǒng)計圖中“基本了解”部分所對應扇形的圓心角的度數.（2）先用接受調查總人數-“基本了解”的人數-“基本了解”的人數-“不了解”的人數，算出“了解”的人數，再根據“了解”的人數補全條形統(tǒng)計圖.（3）利用總人數900乘以“了解”和“基本了解”所對應的百分比即可求解．（4）首先根據題意列出表格，然后由表格求得所有等可能的結果以及一男一女參加比賽的情況，再利用概率公式即可求得答案．

試題解析：（1）60,90°；

（2） 補全條形統(tǒng)計圖如圖所示：

（3） 根據題意得：900×＝300（人），

則估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數為300人．

（4） 列表法如圖所示：

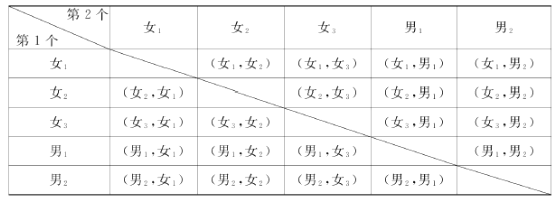
則所有等可能的情況有20種，其中選中1個男生和1個女生的情況有12種，所以恰好抽到1個男生和1個女生的概率：P＝＝.