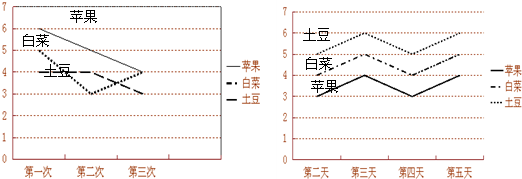
解:(1)根據“第2-5天平均菜價”圖可知,
3元/千克≤蘋果的價格≤4元/千克,
4元/千克≤白菜的價格≤5元/千克,
5元/千克≤土豆的價格≤6元/千克,
所以蘋果的價格最便宜;
(2)根據“第1天菜價調查情況”圖可知,
土豆的價格波動范圍是:4-3=1(元/千克),
白菜的價格波動范圍是:5-3=2(元/千克),
蘋果的價格波動范圍是:6-4=2(元/千克),
所以土豆的價格波動最小;
(3)第1天的平均菜價為:
蘋果:

(6+5+4)=5(元/千克),白菜:

(5+3+4)=4(元/千克),土豆:

(4+4+3)=

(元/千克),
它們在1-5天的平均菜價為:
蘋果:

(5+3+4+3+4)=
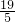
(元/千克),白菜:

(4+4+5+4+5)=

(元/千克),土豆:

(

+5+6+5+6)=
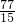
(元/千克);
(4)根據上面第一個圖可知,蘋果在17:00以后價格較低,根據第二個圖可知,蘋果在第二天或第四天價格較低,
所以在3-5天中的第四天的17:00購買蘋果最省錢.
分析:(1)根據“第2-5天平均菜價”圖可知,蘋果的價格最便宜;
(2)根據“第1天菜價調查情況”圖,得出這一天每一種蔬菜的最高價格與最低價格,再用最高價格與最低價格相減比較后即可求出價格波動最小的蔬菜;
(3)先分別求出蘋果、白菜、土豆第1天的平均菜價,再求出它們在1-5天的平均菜價;
(4)根據上面第一個圖可知,蘋果在17:00以后價格較低,根據第二個圖可知,蘋果在第二天或第四天價格較低,進而得出結論.
點評:本題考查了折線圖的意義,平均數和極差的概念.平均數是指在一組數據中所有數據之和再除以數據的個數.平均數是表示一組數據集中趨勢的量數,它是反映數據集中趨勢的一項指標.解答平均數應用題的關鍵在于確定“總數量”以及和總數量對應的總份數.極差是最大值與最小值的差,極差是刻畫數據離散程度的一個統計量,它反映了數據的波動范圍.

 (6+5+4)=5(元/千克),白菜:
(6+5+4)=5(元/千克),白菜: (5+3+4)=4(元/千克),土豆:
(5+3+4)=4(元/千克),土豆: (4+4+3)=
(4+4+3)= (元/千克),
(元/千克), (5+3+4+3+4)=
(5+3+4+3+4)=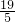 (元/千克),白菜:
(元/千克),白菜: (4+4+5+4+5)=
(4+4+5+4+5)= (元/千克),土豆:
(元/千克),土豆: (
( +5+6+5+6)=
+5+6+5+6)=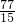 (元/千克);
(元/千克);

 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案