
【題目】求下列各式的值:
(1)x2﹣25=0
(2)x3﹣3= ![]() .
.
【答案】
(1)解:x2﹣25=0,
x2=25,
x=±5
(2)解:x3﹣3= ![]() ,
,
x3= ![]() ,
,
∴x= ![]() ,
,
∴x= ![]()
【解析】(1)先移項,再利用平方根定義開方即可求出解;(2)方程變形后,利用立方根定義開方即可求出解.
【考點精析】根據題目的已知條件,利用平方根的基礎和立方根的相關知識可以得到問題的答案,需要掌握如果一個數的平方等于a,那么這個數就叫做a的平方根(或二次方跟);一個數有兩個平方根,他們互為相反數;零的平方根是零;負數沒有平方根;如果一個數的立方等于a,那么這個數就叫做a 的立方根(或a 的三次方根);一個正數有一個正的立方根;一個負數有一個負的立方根;零的立方根是零.


科目:初中數學 來源: 題型:
【題目】把點(3,-2)關于x軸的對稱點向下平移3個單位,所得點的坐標為( )
A. (6,-2) B. (0,-2) C. (3,-1) D. (3,5)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在△ABC中,E,F分別在AB,AC上,則下列各式不能成立的是( ) 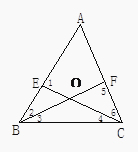
A.∠BOC=∠2+∠6+∠A
B.∠2=∠5-∠A
C.∠5=∠1+∠4
D.∠1=∠ABC+∠4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式中去括號正確的是( )
A. a+(b-c+d)=a-b+c-d B. a-(b-c+d)=a-b-c+d
C. a-(b-c+d)=a-b+c-d D. a-(b-c+d)=a-b+c+d
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內角∠ABC、外角∠ACF.以下結論:
①AD∥BC;②∠ACB=2∠ADB;③∠ADC=90°-∠ABD;④BD平分∠ADC;
⑤∠BDC= ![]() ∠BAC.
∠BAC.
其中正確的結論有( )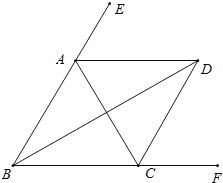
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
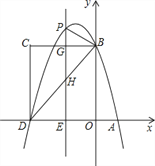
【題目】如圖,在平面直角坐標系中,拋物線y=-![]() x2+bx+c與x軸交于A、D兩點,與y軸交于點B,四邊形OBCD是矩形,點A的坐標為(1,0),點D的坐標為(-3,0),點B的坐標為(0,4),已知點E(m,0)是線段DO上的動點,過點E作PE⊥x軸交拋物線于點P,交BC于點G,交BD于點H.
x2+bx+c與x軸交于A、D兩點,與y軸交于點B,四邊形OBCD是矩形,點A的坐標為(1,0),點D的坐標為(-3,0),點B的坐標為(0,4),已知點E(m,0)是線段DO上的動點,過點E作PE⊥x軸交拋物線于點P,交BC于點G,交BD于點H.
(1)求該拋物線的解析式;
(2)當點P在直線BC上方時,請用含m的代數式表示PG的長度;
(3)在(2)的條件下,是否存在這樣的點P,使得以P、B、G為頂點的三角形與△DEH相似?若存在,求出此時m的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com