
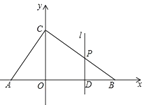
【題目】如圖,在平面直角坐標(biāo)系中,![]() 的斜邊在
的斜邊在![]() 在
在![]() 軸上,點(diǎn)
軸上,點(diǎn)![]() 在
在![]() 軸上
軸上![]() ,
,![]() 、
、![]() 的長分別是一元二次方程
的長分別是一元二次方程![]() 的兩個(gè)根,且
的兩個(gè)根,且![]() .
.
(1)求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)![]() 是線段
是線段![]() 上的一個(gè)動點(diǎn)(點(diǎn)
上的一個(gè)動點(diǎn)(點(diǎn)![]() 不與點(diǎn)
不與點(diǎn)![]() ,
,![]() 重合),過點(diǎn)
重合),過點(diǎn)![]() 的直線
的直線![]() 與
與![]() 軸平行,直線
軸平行,直線![]() 交邊
交邊![]() 或邊
或邊![]() 于點(diǎn)
于點(diǎn)![]() ,設(shè)點(diǎn)
,設(shè)點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() ,線段
,線段![]() 的長為
的長為![]() ,求
,求![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(3)在(2)的條件下,當(dāng)![]() 時(shí),請你直接寫出點(diǎn)P的坐標(biāo).
時(shí),請你直接寫出點(diǎn)P的坐標(biāo).
【答案】(1)![]() ;(2)
;(2)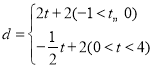 ;(3)
;(3)![]() ,
,![]() 或
或![]()
【解析】
(1)由一元二次方程可求得![]() 、
、![]() 的長,利用
的長,利用![]() 可求得
可求得![]() 的長,則可求得
的長,則可求得![]() 點(diǎn)坐標(biāo);
點(diǎn)坐標(biāo);
(2)由![]() 、
、![]() 、
、![]() 的坐標(biāo)可分別求得直線
的坐標(biāo)可分別求得直線![]() 、
、![]() 的解析式,當(dāng)點(diǎn)
的解析式,當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),則點(diǎn)
上時(shí),則點(diǎn)![]() 在直線
在直線![]() 上,則可表示出
上,則可表示出![]() 點(diǎn)坐標(biāo),從而可表示出
點(diǎn)坐標(biāo),從而可表示出![]() 的長;當(dāng)點(diǎn)
的長;當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),則點(diǎn)
上時(shí),則點(diǎn)![]() 在直線
在直線![]() 上,可表示出點(diǎn)
上,可表示出點(diǎn)![]() 的坐標(biāo),從而可表示出
的坐標(biāo),從而可表示出![]() 的長,即可求得
的長,即可求得![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(3)在(2)中所求的函數(shù)關(guān)系式中分別令![]() ,分別求得相應(yīng)的
,分別求得相應(yīng)的![]() 的值,即可求得
的值,即可求得![]() 點(diǎn)坐標(biāo).
點(diǎn)坐標(biāo).
解:(1)解方程![]() 可得
可得![]() 或
或![]() ,
,
![]() 、
、![]() 的長分別是一元二次方程
的長分別是一元二次方程![]() 的兩個(gè)根,且
的兩個(gè)根,且![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ;
;
(2)由(1)可知![]() ,
,![]() ,
,![]() ,
,
設(shè)直線![]() 解析式為
解析式為![]() ,
,
![]()
![]() ,解得
,解得![]() ,
,
![]() 直線
直線![]() 解析式為
解析式為![]() ,
,
同理可求得直線![]() 解析式為
解析式為![]() ,
,
當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),即
上時(shí),即![]() 時(shí),則點(diǎn)
時(shí),則點(diǎn)![]() 在直線
在直線![]() 上,
上,
![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() ,
,
![]() ;
;
當(dāng)點(diǎn)![]() 在線段
在線段![]() 上時(shí),即
上時(shí),即![]() 時(shí),則點(diǎn)
時(shí),則點(diǎn)![]() 在直線
在直線![]() 上,
上,
![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() ,
,
![]() ;
;
綜上可知![]() 關(guān)于
關(guān)于![]() 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為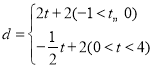 ;
;
(3)在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ;
;
在![]() 中,令
中,令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
![]() ;
;
綜上可知當(dāng)![]() 時(shí),
時(shí),![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() ,
,![]() 或
或![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
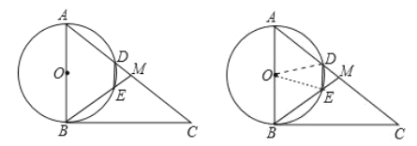
【題目】如圖1,在![]() 中,
中,![]() ,點(diǎn)
,點(diǎn)![]() 是
是![]() 的中點(diǎn),以
的中點(diǎn),以![]() 為直徑做
為直徑做![]() 分別交
分別交![]() ,
,![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() .
.
(1)求證:![]() .
.
(2)如圖2,連![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時(shí),求證:四邊形
時(shí),求證:四邊形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】對于二次函數(shù)y=x2+mx+1,當(dāng)0<x≤2時(shí)的函數(shù)值總是非負(fù)數(shù),則實(shí)數(shù)m的取值范圍為( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩店銷售同一種蔬菜種子.在甲店,不論一次購買數(shù)量是多少,價(jià)格均為4.5元![]() .在乙店價(jià)格為5元
.在乙店價(jià)格為5元![]() ,如果一次購買2kg以上的種子,超出2kg部分的種子價(jià)格打8折.設(shè)小明在同一個(gè)店一次購買種子的數(shù)量為
,如果一次購買2kg以上的種子,超出2kg部分的種子價(jià)格打8折.設(shè)小明在同一個(gè)店一次購買種子的數(shù)量為![]() (
(![]() ).
).
(1)根據(jù)題意填表:
一次購買數(shù)量∕ | 1.5 | 2 | 3.5 | 6 | … |
在甲店花費(fèi)∕元 | 6.75 | 15.75 | … | ||
在乙店花費(fèi)∕元 | 7.5 | 16 | … |
(2)設(shè)在甲店花費(fèi)![]() 元,在乙店花費(fèi)
元,在乙店花費(fèi)![]() 元,分別求
元,分別求![]() ,
,![]() 關(guān)于
關(guān)于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(3)根據(jù)題意填空:
① 若小明在甲店和在乙店一次購買種子的數(shù)量相同,且花費(fèi)相同,則他在同一個(gè)店一次購買種子的數(shù)量為 ![]() ;
;
② 若小明在同一個(gè)店一次購買種子的數(shù)量為3kg,則他在甲、乙兩個(gè)店中的 店購買花費(fèi);
③ 若小明在同一個(gè)店一次購買種子花費(fèi)了45元,則他在甲、乙兩個(gè)店中的 店購買數(shù)量多.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
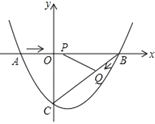
【題目】如圖,在平面直角坐標(biāo)系中,拋物線![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() .
.
(1)求拋物線的解析式;
(2)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),在線段
點(diǎn)出發(fā),在線段![]() 上以每秒3個(gè)單位長度的速度向
上以每秒3個(gè)單位長度的速度向![]() 點(diǎn)運(yùn)動,同時(shí)點(diǎn)
點(diǎn)運(yùn)動,同時(shí)點(diǎn)![]() 從
從![]() 點(diǎn)出發(fā),在線段
點(diǎn)出發(fā),在線段![]() 上以每秒1個(gè)單位長度的速度向
上以每秒1個(gè)單位長度的速度向![]() 點(diǎn)運(yùn)動,其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí),另一個(gè)點(diǎn)也停止運(yùn)動,當(dāng)
點(diǎn)運(yùn)動,其中一個(gè)點(diǎn)到達(dá)終點(diǎn)時(shí),另一個(gè)點(diǎn)也停止運(yùn)動,當(dāng)![]() 存在時(shí),求運(yùn)動多少秒使
存在時(shí),求運(yùn)動多少秒使![]() 的面積最大,最大面積是多少?
的面積最大,最大面積是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
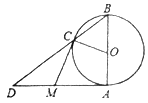
【題目】如圖,![]() 是
是![]() 的直徑,且
的直徑,且![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 外一點(diǎn),且
外一點(diǎn),且![]() ,
,![]() 分別切
分別切![]() 于點(diǎn)
于點(diǎn)![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).![]() 與
與![]() 的延長線交于點(diǎn)
的延長線交于點(diǎn)![]() .
.
(1)求證:![]() ;
;
(2)填空
①當(dāng)![]() ________時(shí),四邊形
________時(shí),四邊形![]() 是正方形.
是正方形.
②當(dāng)![]() _________時(shí),
_________時(shí),![]() 為等邊三角形.
為等邊三角形.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】課前預(yù)習(xí)是學(xué)習(xí)數(shù)學(xué)的重要環(huán)節(jié),為了了解所教班級學(xué)生完成數(shù)學(xué)課前預(yù)習(xí)的具體情況,王老師對本班部分學(xué)生進(jìn)行了為期一個(gè)月的跟蹤調(diào)查.她將調(diào)查結(jié)果分為四類,![]() :優(yōu)秀;
:優(yōu)秀;![]() :良好:
:良好:![]() :一般;
:一般;![]() :較差,并將調(diào)查結(jié)果繪制成以下兩幅不完整的統(tǒng)計(jì)圖,請你解答下列問題:
:較差,并將調(diào)查結(jié)果繪制成以下兩幅不完整的統(tǒng)計(jì)圖,請你解答下列問題:

(1)將條形統(tǒng)計(jì)圖補(bǔ)充完整;
(2)為了共同進(jìn)步,王老師想從被調(diào)查的![]() 類和
類和![]() 類學(xué)生中各隨機(jī)選取一位同學(xué)進(jìn)行“一幫一”互助學(xué)習(xí),請用列表法或畫樹形圖的方法求出所選兩位同學(xué)恰好是異性的概率;
類學(xué)生中各隨機(jī)選取一位同學(xué)進(jìn)行“一幫一”互助學(xué)習(xí),請用列表法或畫樹形圖的方法求出所選兩位同學(xué)恰好是異性的概率;
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
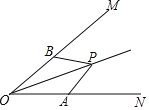
【題目】如圖,點(diǎn)P在∠MON的平分線上,點(diǎn)A、B在∠MON的兩邊上,若要使△AOP≌△BOP,那么需要添加一個(gè)條件是_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+3(a≠0)經(jīng)過點(diǎn)A(1,0)和點(diǎn)B(3,0),與y軸交于點(diǎn)C.
(1)求此拋物線的解析式;
(2)若點(diǎn)P是直線BC下方的拋物線上一動點(diǎn)(不點(diǎn)B,C重合),過點(diǎn)P作y軸的平行線交直線BC于點(diǎn)D,設(shè)點(diǎn)P的橫坐標(biāo)為m.
①用含m的代數(shù)式表示線段PD的長.
②連接PB,PC,求△PBC的面積最大時(shí)點(diǎn)P的坐標(biāo).
(3)設(shè)拋物線的對稱軸與BC交于點(diǎn)E,點(diǎn)M是拋物線的對稱軸上一點(diǎn),N為y軸上一點(diǎn),是否存在這樣的點(diǎn)M和點(diǎn)N,使得以點(diǎn)C、E、M、N為頂點(diǎn)的四邊形是菱形?如果存在,請直接寫出點(diǎn)M的坐標(biāo);如果不存在,請說明理由.

查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com