
【題目】心理學(xué)研究發(fā)現(xiàn),一般情況下,在一節(jié)![]() 分鐘的課中,學(xué)生的注意力隨學(xué)習(xí)時間的變化而變化.開始學(xué)習(xí)時,學(xué)生的注意力逐步增強,中間有一段時間學(xué)生的注意力保持較為理想的穩(wěn)定狀態(tài),隨后學(xué)生的注意力開始分散.經(jīng)過實驗分析可知,學(xué)生的注意力指標數(shù)
分鐘的課中,學(xué)生的注意力隨學(xué)習(xí)時間的變化而變化.開始學(xué)習(xí)時,學(xué)生的注意力逐步增強,中間有一段時間學(xué)生的注意力保持較為理想的穩(wěn)定狀態(tài),隨后學(xué)生的注意力開始分散.經(jīng)過實驗分析可知,學(xué)生的注意力指標數(shù)![]() 隨時間
隨時間![]() (分鐘)的變化規(guī)律如下圖所示(其中
(分鐘)的變化規(guī)律如下圖所示(其中![]() 、
、![]() 分別為線段,
分別為線段,![]() 為雙曲線的一部分).
為雙曲線的一部分).
![]() 求注意力指標數(shù)
求注意力指標數(shù)![]() 與時間
與時間![]() (分鐘)之間的函數(shù)關(guān)系式;
(分鐘)之間的函數(shù)關(guān)系式;
![]() 開始學(xué)習(xí)后第
開始學(xué)習(xí)后第![]() 分鐘時與第
分鐘時與第![]() 分鐘時相比較,何時學(xué)生的注意力更集中?
分鐘時相比較,何時學(xué)生的注意力更集中?
![]() 某些數(shù)學(xué)內(nèi)容的課堂學(xué)習(xí)大致可分為三個環(huán)節(jié):即“教師引導(dǎo),回顧舊知;自主探索,合作交流;總結(jié)歸納,鞏固提高”.其中“教師引導(dǎo),回顧舊知”環(huán)節(jié)
某些數(shù)學(xué)內(nèi)容的課堂學(xué)習(xí)大致可分為三個環(huán)節(jié):即“教師引導(dǎo),回顧舊知;自主探索,合作交流;總結(jié)歸納,鞏固提高”.其中“教師引導(dǎo),回顧舊知”環(huán)節(jié)![]() 分鐘;重點環(huán)節(jié)“自主探索,合作交流”這一過程一般
分鐘;重點環(huán)節(jié)“自主探索,合作交流”這一過程一般

需要![]() 分鐘才能完成,為了確保效果,要求學(xué)習(xí)時的注意力指標數(shù)不低于
分鐘才能完成,為了確保效果,要求學(xué)習(xí)時的注意力指標數(shù)不低于![]() .請問這樣的課堂學(xué)習(xí)安排是否合理?并說明理由.
.請問這樣的課堂學(xué)習(xí)安排是否合理?并說明理由.
【答案】(1)![]() ,
,![]() ,
,![]() (2)第
(2)第![]() 分鐘時學(xué)生的注意力更集中(3)這樣的課堂學(xué)習(xí)安排不合理
分鐘時學(xué)生的注意力更集中(3)這樣的課堂學(xué)習(xí)安排不合理
【解析】
(1)從圖象上看,AB表示的函數(shù)為一次函數(shù),BC是平行于x軸的線段,CD為雙曲線的一部分,設(shè)出解析式,代入數(shù)值可以解答;
(2)把自變量的值代入相對應(yīng)的函數(shù)解析式,求出對應(yīng)的函數(shù)值比較得出;
(3)求出相對應(yīng)的自變量的值,代入相對應(yīng)的函數(shù)解析式,求出注意力指標數(shù)與40相比較,得出答案.
解:![]() 設(shè)
設(shè)![]() ,把
,把![]() ,
,![]() 代入函數(shù)解析式解得
代入函數(shù)解析式解得![]() ,
,
由圖象直接得到![]() ,
,
設(shè)![]() ,把
,把![]() 代入函數(shù)解析式解得
代入函數(shù)解析式解得![]() ;
;
![]() 把
把![]() 代入
代入![]() ,得
,得![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,
,
因為![]() ,
,
所以第![]() 分鐘時學(xué)生的注意力更集中;
分鐘時學(xué)生的注意力更集中;
![]() 不合理.
不合理.
因為![]() 分鐘,把
分鐘,把![]() 代入
代入![]() ,
,
解得![]() ,
,
所以這樣的課堂學(xué)習(xí)安排不合理.


 時刻準備著暑假作業(yè)原子能出版社系列答案
時刻準備著暑假作業(yè)原子能出版社系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】銷售某種商品,根據(jù)經(jīng)驗,銷售單價不少于30元 /件,但不超過50元 /件時,銷售數(shù)量N (件)與商品單價M (元 /件)的函數(shù)關(guān)系的圖象如圖所示中的線段AB.

(1)求y關(guān)于x的函數(shù)關(guān)系式;
(2)如果計劃每天的銷售額為2400元時,那么該商品的單價應(yīng)該定多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖16,拋物線y=ax2+3ax+c(a>0)與y軸交于點C,與x軸交于A,B兩點,點A在點B左側(cè).點B的坐標為(1,0),OC=3OB.
(1)求拋物線的解析式.
(2)若點D是線段AC下方拋物線上的動點,求四邊形ABCD面積的最大值.
(3)若點E在x軸上,點P在拋物線上.是否存在以A,C,E,P為頂點且以AC為一邊的平行四邊形?若存在,求出點P的坐標;若不存在,請說明理由.


查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)活動–探究特殊的平行四邊形.
問題情境
如圖,在四邊形![]() 中,
中,![]() 為對角線,
為對角線,![]() ,
,![]() .請你添加條件,使它們成為特殊的平行四邊形.
.請你添加條件,使它們成為特殊的平行四邊形.
提出問題

![]() 第一小組添加的條件是“
第一小組添加的條件是“![]() ”,則四邊形
”,則四邊形![]() 是菱形.請你證明;
是菱形.請你證明;
![]() 第二小組添加的條件是“
第二小組添加的條件是“![]() ,
,![]() ”,則四邊形
”,則四邊形![]() 是正方形.請你證明.
是正方形.請你證明.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有一個安裝有進出水管的30升容器,水管每單位時間內(nèi)進出的水量是一定的,設(shè)從某時刻開始的4分鐘內(nèi)只進水不出水,在隨后的8分鐘內(nèi)既進水又出水,得到水量y(升)與時間x(分)之間的函數(shù)關(guān)系如圖所示根據(jù)圖象信息給出下列說法:
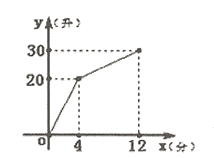
①每分鐘進水5升;
②當(dāng)![]() 時,容器中水量在減少;
時,容器中水量在減少;
③若12分鐘后只放水,不進水,還要8分鐘可以把水放完;
④若從一開始進出水管同時打開需要24分鐘可以將容器灌滿.
以下說法中正確的有( )
A.①B.①②C.①④D.①②④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 中,
中,![]() ,
,![]() .
.![]() ,點
,點![]() 是
是![]() 上一點,以
上一點,以![]() 為圓心作
為圓心作![]() ,
,
![]() 若
若![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點,求
兩點,求![]() 的半徑,并判斷點
的半徑,并判斷點![]() 與
與![]() 的位置關(guān)系.
的位置關(guān)系.
![]() 若
若![]() 和
和![]() 、
、![]() 都相切,求
都相切,求![]() 的半徑.
的半徑.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四邊形ABCD中,點E、F是BC、CD的中點,且AE⊥BC,AF⊥CD.

(1)求證:AB=AD.
(2)請你探究∠EAF,∠BAE,∠DAF之間有什么數(shù)量關(guān)系?并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,lA、lB分別表示A步行與B騎車在同一路上行駛的路程S與時間t的關(guān)系.

(1)B出發(fā)時與A相距______千米;
(2)走了一段路后,自行車發(fā)生故障,進行修理,所用的時間是______小時;
(3)B再次出發(fā)后______小時與A相遇;
(4)求出A行走的路程S與時間t的函數(shù)關(guān)系式(寫出過程);
(5)若B的自行車不發(fā)生故障,保持出發(fā)時的速度前進,幾小時與A相遇?在圖中表示出這個相遇點C.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩同學(xué)從A地出發(fā),騎自行車在同一條路上行駛到B地,他們離出發(fā)地的距離s(千米)和行駛時間t(小時)之間的函數(shù)關(guān)系圖象如圖所示,根據(jù)圖中提供的信息,有下列說法:

(1)他們都行駛了18千米;
(2)甲在途中停留了0.5小時;
(3)乙比甲晚出發(fā)了0.5小時;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙兩人同時到達目的地
其中符合圖象描述的說法有( )
A. 2個B. 3個C. 4個D. 5個
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com