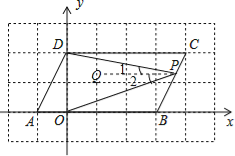
【題目】(10分)如圖，在直角坐標系xOy中，A(﹣1，0)，B(3，0)，將A，B同時分別向上平移2個單位，再向右平移1個單位，得到的對應點分別為D，C，連接AD，BC.
(1)直接寫出點C，D的坐標：C ，D ；
(2)四邊形ABCD的面積為 ；
(3)點P為線段BC上一動點(不含端點)，連接PD，PO.求證：∠CDP+∠BOP=∠OPD.
【答案】(1)(4，2)，(0，2)；(2)8；(3)見解析
【解析】試題分析：（1）根據C、D兩點在坐標系中的位置即可得出此兩點坐標；
（2）先判斷出四邊形ABCD是平行四邊形，再求出其面積即可；
（3）過點P作PQ∥AB，故可得出CD∥PQ，AB∥PQ，由平形線的性質即可得出結論．
解：（1）由圖可知，C（4，2），D（0，2）．
故答案為：（4，2），（0，2）；
（2）∵線段CD由線段BA平移而成，
∴AB∥CD，AB=CD，
∴四邊形ABCD是平行四邊形，
∴S平行四邊形ABCD=4×2=8．
故答案為：8；
（3）證明：如圖，過點P作PQ∥AB，
∵CD∥AB，
∴CD∥PQ，AB∥PQ，
∴∠CDP=∠1，∠BOP=∠2，
∴∠CDP+∠BOP=∠1+∠2=∠OPD．
口算題卡加應用題集訓系列答案
綜合自測系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知點A（0，2），B（2，2），C（﹣1，﹣2），拋物線F：y=x2﹣2mx+m2﹣2與直線x=﹣2交于點P．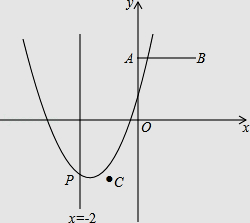 
（1）當拋物線F經過點C時，求它的表達式；
（2）設點P的縱坐標為yP ， 求yP的最小值，此時拋物線F上有兩點（x1 ， y1），（x2 ， y2），且x1＜x2≤﹣2，比較y1與y2的大小；
（3）當拋物線F與線段AB有公共點時，直接寫出m的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我們知道對于一個圖形，通過不同的方法計算圖形的面積可以得到一個數學等式．
例如：由圖1可得到(a+b)=a+2ab+b．
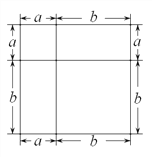
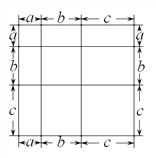
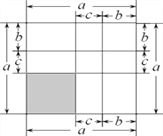
圖1 圖2 圖3
（1）寫出由圖2所表示的數學等式：_____________________；寫出由圖3所表示的數學等式：_____________________；
（2）利用上述結論，解決下面問題：已知a+b+c=11，bc+ac+ab=38，求a+b+c的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小敏從A地出發向B地行走，同時小聰從B地出發向A地行走，如圖所示，相交于點P的兩條線段
、
分別表示小敏、小聰離B地的距離
與已用時間
之間的關系，則小敏、小聰行走的速度分別是
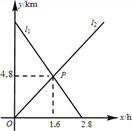
A. 
和
B. 
和
C. 
和
D. 
和
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，O為坐標原點， 
的圓心坐標為
，半徑為
函數
的圖象與x軸交于點A，與y軸交于點B，點P為線段AB上一動點．
連接CO，求證： 
；
若
是等腰三角形，求點P的坐標；
當直線PO與
相切時，求
的度數；當直線PO與
相交時，設交點為E、F，點M為線段EF的中點，令
，求s與t之間的函數關系，并寫出t的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】設A（-2，y1），B（1，y2），C（2，y3）是拋物線y=-（x+1）2+a上的三點，則y1 ， y2 ， y3的大小關系為（ ）
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y3>y1>y2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：用2輛A型車和1輛B型車裝滿貨物一次可運貨10噸；用1輛A型車和2輛B型車裝滿貨物一次可運貨11噸．某物流公司現有31噸貨物，計劃同時租用A型車
輛，B型車
輛，一次運完，且恰好每輛車都裝滿貨物． 根據以上信息，解答下列問題：
（1）1輛A型車和1輛B型車都裝滿貨物一次可分別運貨多少噸？
（2）請你幫該物流公司設計租車方案．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
