
【題目】如圖,長方形OABC的OA邊在x軸的正半軸上,OC在y軸的正半軸上,拋物線y=ax2+bx經過點B(1,4)和點E(3,0)兩點.
(1)求拋物線的解析式;
(2)若點D在線段OC上,且BD⊥DE,BD=DE,求D點的坐標;
(3)在條件(2)下,在拋物線的對稱軸上找一點M,使得△BDM的周長為最小,并求△BDM周長的最小值及此時點M的坐標;
(4)在條件(2)下,從B點到E點這段拋物線的圖象上,是否存在一個點P,使得△PAD的面積最大?若存在,請求出△PAD面積的最大值及此時P點的坐標;若不存在,請說明理由.
【答案】
(1)解:將點B(1,4),E(3,0)的坐標代入拋物線的解析式得: ![]() ,
,
解得: ![]() ,
,
拋物線的解析式為y=﹣2x2+6x
(2)解:如圖1所示;

∵BD⊥DE,
∴∠BDE=90°.
∴∠BDC+∠EDO=90°.
又∵∠ODE+∠DEO=90°,
∴∠BDC=∠DE0.
在△BDC和△DOE中, 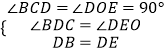 ,
,
∴△BDC≌△DEO.
∴OD=AO=1.
∴D(0,1)
(3)解:如圖2所示:作點B關于拋物線的對稱軸的對稱點B′,連接B′D交拋物線的對稱軸與點M.
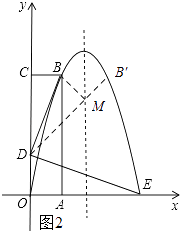
∵x=﹣ ![]() =
= ![]() ,
,
∴點B′的坐標為(2,4).
∵點B與點B′關于x= ![]() 對稱,
對稱,
∴MB=B′M.
∴DM+MB=DM+MB′.
∴當點D、M、B′在一條直線上時,MD+MB有最小值(即△BMD的周長有最小值).
∵由兩點間的距離公式可知:BD= ![]() =
= ![]() ,DB′=
,DB′= ![]() =
= ![]() ,
,
∴△BDM的最小值= ![]() +
+ ![]() .
.
設直線B′D的解析式為y=kx+b.
將點D、B′的坐標代入得: ![]() ,
,
解得:k= ![]() ,b=1.
,b=1.
∴直線DB′的解析式為y= ![]() x+1.
x+1.
將x= ![]() 代入得:y=
代入得:y= ![]() .
.
∴M( ![]() ,
, ![]() )
)
(4)解:如圖3所示:過點F作FG⊥x軸,垂足為G.
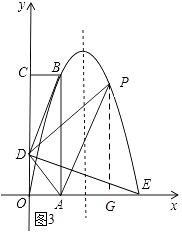
設點P(a,﹣2a2+6a),則OG=a,PG=﹣2a2+6a.
∵S梯形DOGP= ![]() (OD+PG)OG=
(OD+PG)OG= ![]() (﹣2a2+6a+1)×a=﹣a3+3a2+
(﹣2a2+6a+1)×a=﹣a3+3a2+ ![]() a,S△ODA=
a,S△ODA= ![]() ODOA=
ODOA= ![]() ×1×1=
×1×1= ![]() ,S△AGP=
,S△AGP= ![]() AGPG=﹣a3+4a2﹣3a,
AGPG=﹣a3+4a2﹣3a,
∴S△PDA=S梯形DOGP﹣S△ODA﹣S△AGP=﹣a2+ ![]() a﹣
a﹣ ![]() .
.
∴當a= ![]() 時,S△PDA的最大值為
時,S△PDA的最大值為 ![]() .
.
∴點P的坐標為( ![]() ,
, ![]() )
)
【解析】(1)將點B(1,4),E(3,0)的坐標代入拋物線的解析式,得到關于a、b的方程組,求得a、b的值,從而可得到拋物線的解析式;(2)依據同角的余角相等證明∠BDC=∠DE0,然后再依據AAS證明△BDC≌△DEO,從而得到OD=AO=1,于是可求得點D的坐標;(3)作點B關于拋物線的對稱軸的對稱點B′,連接B′D交拋物線的對稱軸與點M.先求得拋物線的對稱軸方程,從而得到點B′的坐標,由軸對稱的性質可知當點D、M、B′在一條直線上時,△BMD的周長有最小值,依據兩點間的距離公式求得BD和B′D的長度,從而得到三角形的周長最小值,然后依據待定系數法求得D、B′的解析式,然后將點M的橫坐標代入可求得點M的縱坐標;(4)過點F作FG⊥x軸,垂足為G.設點F(a,﹣2a2+6a),則OG=a,FG=﹣2a2+6a.然后依據S△FDA=S梯形DOGF﹣S△ODA﹣S△AGF的三角形的面積與a的函數關系式,然后依據二次函數的性質求解即可.


科目:初中數學 來源: 題型:
【題目】如圖,我們把杜甫(絕句)整齊排列放在平面直角坐標系中:

(1)“東”、“窗”和“柳”的坐標依次是:______、______和________.;
(2)將第1行與第3行對調,再將第4列與第6列對調,“里”由開始的坐標________依次變換到:________和________;
(3)“門”開始的坐標是(1,1),使它的坐標到(3,2),應該哪兩行對調,同時哪兩列對調?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在⊙O的內接四邊形ACDB中,AB為直徑,AC:BC=1:2,點D為弧AB的中點,BE⊥CD垂足為E. 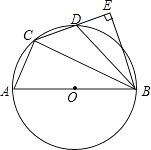
(1)求∠BCE的度數;
(2)求證:D為CE的中點;
(3)連接OE交BC于點F,若AB= ![]() ,求OE的長度.
,求OE的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司招聘職員兩名,對甲、乙、丙、丁四名候選人進行了筆試和面試,各項成績滿分均為100分,然后再按筆試占60%、面試占40%計算候選人的綜合成績(滿分為100分).
他們的各項成績如下表所示:
候選人 | 筆試成績/分 | 面試成績/分 |
甲 | 90 | 88 |
乙 | 84 | 92 |
丙 | x | 90 |
丁 | 88 | 86 |
(1)直接寫出這四名候選人面試成績的中位數;
(2)現得知候選人丙的綜合成績為87.6分,求表中x的值;
(3)求出其余三名候選人的綜合成績,并以綜合成績排序確定所要招聘的前兩名的人選.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是橘子的銷售額隨橘子賣出質量的變化表:
質量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
銷售額/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)這個表反映了哪兩個變量之間的關系?哪個是自變量?哪個是因變量?
(2)當橘子賣出5千克時,銷售額是_______元.
(3)如果用![]() 表示橘子賣出的質量,
表示橘子賣出的質量,![]() 表示銷售額,按表中給出的關系,
表示銷售額,按表中給出的關系,![]() 與
與![]() 之間的關系式為______.
之間的關系式為______.
(4)當橘子的銷售額是100元時,共賣出多少千克橘子?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】乘法公式的探究及應用.
(1)如圖1,可以求出陰影部分的面積是 (寫成兩數平方差的形式);
(2)如圖2,若將陰影部分裁剪下來,重新拼成一個矩形,它的寬是 ,長是 ,面積是 (寫成多項式乘法的形式);
(3)比較圖1、圖2兩圖的陰影部分面積,可以得到乘法公式 (用式子表達);
(4)運用你所得到的公式,計算下列各題:
①(2m+n-p)(2m-n+p);②10.3×9.7.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB、CD相交于點O,過點O作兩條射線OM、ON,且∠AOM=∠CON=90°

(1)若OC平分∠AOM,求∠AOD的度數.
(2)若∠1=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】基本圖形:在Rt△![]() 中,
中,![]() ,
,![]() 為
為![]() 邊上一點(不與點
邊上一點(不與點![]() ,
,![]() 重合),將線段
重合),將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() .
.
探索:(1)連接![]() ,如圖①,試探索線段
,如圖①,試探索線段![]() 之間滿足的等量關系,并證明結論;
之間滿足的等量關系,并證明結論;
(2)連接![]() ,如圖②,試探索線段
,如圖②,試探索線段![]() 之間滿足的等量關系,并證明結論;
之間滿足的等量關系,并證明結論;

聯想:(3)如圖③,在四邊形![]() 中,
中,![]() .若
.若![]() ,
,![]() ,則
,則![]() 的長為 .
的長為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com