
【題目】觀察下列兩個等式:![]() ,
,![]() ,給出定義如下:我們稱使等式ab=ab+1成立的一對有理數a,b為“共生有理數對”,記為(a,b),如:數對(2,
,給出定義如下:我們稱使等式ab=ab+1成立的一對有理數a,b為“共生有理數對”,記為(a,b),如:數對(2,![]() ),(5,
),(5,![]() ),都是“共生有理數對”.
),都是“共生有理數對”.
(1)數對(2,1),(3,![]() )中是“共生有理數對”的是_____________;
)中是“共生有理數對”的是_____________;
(2)若(m,n)是“共生有理數對”,則(n,m)_____“共生有理數對”(填“是”或“不是”);說明理由;
(3)若(a,3)是“共生有理數對”,求a的值.
【答案】(1)(3,![]() );(2)是;(3)a=﹣2.
);(2)是;(3)a=﹣2.
【解析】
(1)根據“共生有理數對”的定義即可判斷;
(2)根據“共生有理數對”的定義即可判斷;
(3)根據“共生有理數對”的定義,構建方程即可解決問題.
(1)﹣2﹣1=﹣3,﹣2×1+1=1,∴﹣2﹣1≠﹣2×1+1,∴(﹣2,1)不是“共生有理數對”.
∵3![]() ,3
,3![]() 1
1![]() ,∴3
,∴3![]() 3
3![]() 1,∴(3,
1,∴(3,![]() )是“共生有理數對”;
)是“共生有理數對”;
(2)是.
理由:﹣m﹣(﹣n)=﹣n+m,﹣n(﹣m)+1=mn+1.
∵(m,n)是“共生有理數對”,∴m﹣n=mn+1,∴﹣n+m=mn+1,∴(﹣n,﹣m)是“共生有理數對”.
故答案為:是.
(3)由題意得:a﹣3=3a+1,解得:a=﹣2.


科目:初中數學 來源: 題型:
【題目】探究思考:(本題直接填空,不必寫出解題過程)
問題:在數軸上,點A表示的數為![]() ,則到點A的距離等于3的點所表示的數是 ;
,則到點A的距離等于3的點所表示的數是 ;
變式思考一:如圖1,在數軸上有六個點A、B、C、D、E、F,且相鄰兩點間距離相等,若點A表示的數是![]() ,點F表示的數為11,則與點C表示的數最近的整數是 ;
,點F表示的數為11,則與點C表示的數最近的整數是 ;
![]()
變式思考二:已知數軸上有A、B、C三點,分別代表![]() ,電子螞蟻從A向點C方向以4個單位/秒的速度爬行.則爬行到 秒時,電子螞蟻到A、B、C的距離和為40個單位.
,電子螞蟻從A向點C方向以4個單位/秒的速度爬行.則爬行到 秒時,電子螞蟻到A、B、C的距離和為40個單位.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,網格中每一個小正方形的邊長為1個單位長度.可以利用平面直角坐標系的知識回答以下問題:
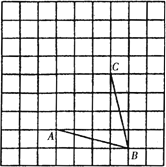
(1)請在所給的網格內畫出以線段AB、BC為邊的平行四邊形ABCD;
(2)填空:平行四邊形ABCD的面積等于____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖E是平行四邊形![]() 邊BC上一點,且
邊BC上一點,且![]() ,連接AE,并延長AE與DC的延長線交于點F,
,連接AE,并延長AE與DC的延長線交于點F, ![]() .
.
(1)請判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(2)求![]() 的各內角的大小.
的各內角的大小.
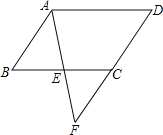
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列解題過程:
計算:(-5)÷![]() ×20.
×20.
解:原式=(-5)÷![]() ×20 (第一步)
×20 (第一步)
=(-5)÷(-1) (第二步)
=-5. (第三步)
(1)上述解題過程中有兩處錯誤:
第一處是第________步,錯誤的原因是__________________________;
第二處是第________步,錯誤的原因是_______________________.
(2)把正確的解題過程寫出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個迷你數獨,圖中實線劃分的區域是一個宮,共有4個宮,每一宮又被虛線分為四個小格.根據圖中已經給的提示數字,在其他的空格上填入-1、-2、-3、-4的數字.使-1、-2、-3、-4每個數字在每一行、每一列和每一宮中都只出現一次。則圖中點A的位置所填的數字為 ( )

A. -1B. -2C. -3D. -4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】股民吉姆上星期買進某公司月股票![]() 股,每股
股,每股![]() 元,下表為本周內每日該股的漲跌情況(星期六、日股市休市)(單位:元)
元,下表為本周內每日該股的漲跌情況(星期六、日股市休市)(單位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股漲跌 | +1.5 | ﹣0.7 | ﹣1.2 | +2 | ﹣1.8 |
(1)星期三收盤時,每股是多少元?
(2)本周內每股最高價多少元?最低價是多少元?
(3)已知吉姆買進股票時付了![]() 的手續費,賣出時還需付成交額
的手續費,賣出時還需付成交額![]() 的手續費和的
的手續費和的![]() 交易稅,如果吉姆在星期五收盤前將全部股票賣出,他的收益情況如何?
交易稅,如果吉姆在星期五收盤前將全部股票賣出,他的收益情況如何?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com