【題目】（2011?常州）如圖，DE是⊙O的直徑，弦AB⊥CD，垂足為C，若AB=6，CE=1，則OC= ，CD= ．
【答案】4；9
【解析】
連接OA構成直角三角形，先根據垂徑定理，由DE垂直AB得到點C為AB的中點，由AB=6可求出AC的長，再設出圓的半徑OA為x，表示出OC，根據勾股定理建立關于x的方程，求出方程的解即可得到x的值，即為圓的半徑，通過觀察圖形可知，OC等于半徑減1，CD等于半徑加OC，把求出的半徑代入即可得到答案．
解：連接OA，
∵直徑DE⊥AB，且AB=6
∴AC=BC=3，
設圓O的半徑OA的長為x，則OE=OD=x
∵CE=1，
∴OC=x-1，
在Rt△AOC中，根據勾股定理得：
x2-（x-1）2=32，化簡得：x2-x2+2x-1=9，
即2x=10，
解得：x=5
所以OE=5，則OC=OE-CE=5-1=4，CD=OD+OC=9．
故答案為：4；9
科目：初中數學 來源： 題型：
【題目】高速鐵路列車（簡稱：高鐵）是人們出行的重要交通工具：已知高鐵平均速度是普通鐵路列車（簡稱：普客）平均速度的的3倍．同樣行駛690km，高鐵比普客少用4.6h．
（1）求高鐵的平均速度．
（2）某天王老師乘坐8：40出發的高鐵，到里程1050km的A市參加當天14：00召開的會議．若他從A市高鐵站到會議地點最多還需要1.5h，試問在高鐵準點到達的情況下，他能在開會之前趕到會議地點嗎？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，學校環保社成員想測量斜坡CD旁一棵樹AB的高度，他們先在點C處測得樹頂B的仰角為60°，然后在坡頂D測得樹頂B的仰角為30°，已知DE⊥EA，斜坡CD的長度為30m，DE的長為15m，則樹AB的高度是_____m．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知，△ABC中，∠ACB=90°，AC=BC，點E是BC上一點，連接AE．
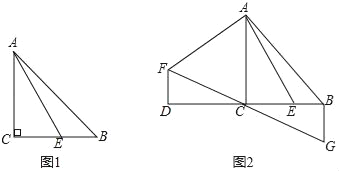
（1）如圖1，當∠BAE=15°，CE=
時，求AB的長．
（2）如圖2，延長BC至D，使DC=BC，將線段AE繞點A順時針旋轉90°得線段AF，連接DF，過點B作BG⊥BC，交FC的延長線于點G，求證：BG=BE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，反比例函數y=
（k≠0）的圖象與一次函數y=ax+b（a≠0）的圖象交于A、B兩點，過點A作AH⊥y軸，垂足為H，若OH=4，sin∠AOH=
，點B的坐標（6，n）．
（1）求反比例函數和一次函數的解析式．
（2）求△AOB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，BD，CE分別是AC，AB邊上的高，BD， CE交于O，則圖中共有相似三角形（ ）
A. 5對 B. 6對 C. 7對 D. 8對
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：在△ABC中，AB=13，BC=12，點D，E分別是AB，BC的中點，連接DE，CD，如果DE=2.5，那么△ACD的周長是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解某校九年級男生的體能情況，體育老師隨機抽取部分男生進行引體向上測試，并對成績進行了統計，繪制出如下的統計圖①和圖②，請跟進相關信息，解答下列問題：
（Ⅰ）本次抽測的男生人數為 ，圖①中m的值為 ；
（Ⅱ）求本次抽測的這組數據的平均數、眾數和中位數；
（Ⅲ）若規定引體向上5次以上（含5次）為體能達標，根據樣本數據，估計該校350名九年級男生中有多少人體能達標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB＝1，AD＝
，BD＝2，∠ABC＋∠ADC＝180°，CD＝
．
（1）判斷△ABD的形狀，并說明理由；
（2）求BC的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com