
【題目】如圖所示,在![]() 中,
中,![]() ,
,![]() ,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N再分別以MN為圓心,大于
,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N再分別以MN為圓心,大于![]() 的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列說法中正確的有________.
的長為半徑畫弧,兩弧交于點P,連接AP并延長交BC于點D,則下列說法中正確的有________.
①AD是![]() 的平分線;②
的平分線;②![]() ;③點D在AB的中垂線上;④
;③點D在AB的中垂線上;④![]()

【答案】①②③④
【解析】
①根據(jù)題目中尺規(guī)作圖的步驟即可判斷出AD是![]() 的平分線;
的平分線;
②利用直角三角形兩銳角互余求出![]() 的度數(shù),然后根據(jù)角平分線的定義求出
的度數(shù),然后根據(jù)角平分線的定義求出![]() 的度數(shù),再根據(jù)直角三角形兩銳角互余即可得出結(jié)論;
的度數(shù),再根據(jù)直角三角形兩銳角互余即可得出結(jié)論;
③通過角平分線的定義能夠得出![]() ,則
,則![]() 然后根據(jù)垂直平分線性質(zhì)定理的逆定理即可得出結(jié)論;
然后根據(jù)垂直平分線性質(zhì)定理的逆定理即可得出結(jié)論;
④根據(jù)含30°的直角三角形的性質(zhì)得出![]() ,則
,則![]() ,又因為
,又因為![]() 和
和![]() 高相同,則
高相同,則![]() 和
和![]() 面積之間的關系可求.
面積之間的關系可求.
由題干可知,AD是![]() 的平分線,故①正確;
的平分線,故①正確;
∵![]() ,
,![]()
∴![]()
∵AD平分∠BAC
∴![]()
![]() , 故②正確;
, 故②正確;
![]()
![]()
∴點D在AB的中垂線上,故③正確;
![]()
![]()
∵![]() 和
和![]() 高相同,
高相同,
∴![]() ,故④正確;
,故④正確;
故答案為:①②③④.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知,如圖,二次函數(shù)y=ax2+bx+c的圖象與x軸交于A、B兩點,其中A點坐標為(﹣1,0),點C(0,5),另拋物線經(jīng)過點(1,8),M為它的頂點.
(1)求拋物線的解析式;
(2)求直線BC的解析式;
(3)求△MCB的面積.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
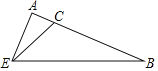
【題目】如圖,Rt△ABE中,∠A=90°,點C在AB上,∠CEB=2∠AEC=45°.
(1)求∠B的度數(shù);
(2)求證:BC=2AE.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中點,CE⊥BD
(1)求證:△ABD≌△BCE.
(2)求證:AC是線段ED的垂直平分線.
(3)△DBC是等腰三角形嗎?請說明理由.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖①,在直角坐標系中,點A的坐標為(1,0),以OA為邊在第一象限內(nèi)作正方形OABC,點D是x軸正半軸上一動點(OD>1),連接BD,以BD為邊在第一象限內(nèi)作正方形DBFE,設M為正方形DBFE的中心,直線MA交y軸于點N.如果定義:只有一組對角是直角的四邊形叫做損矩形.
(1)試找出圖1中的一個損矩形;
(2)試說明(1)中找出的損矩形的四個頂點一定在同一個圓上;
(3)隨著點D位置的變化,點N的位置是否會發(fā)生變化?若沒有發(fā)生變化,求出點N的坐標;若發(fā)生變化,請說明理由;
(4)在圖②中,過點M作MG⊥y軸于點G,連接DN,若四邊形DMGN為損矩形,求D點坐標.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖三角形ABC中,AB=3,AC=4,以BC為邊向三角形外作等邊三角形BCD,連AD,則當∠BAC=_____度時,AD有最大值_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】甲、乙兩車分別從![]() 地將一批物資運往
地將一批物資運往![]() 地,兩車離
地,兩車離![]() 地的距離
地的距離![]() (千米)與其相關的時間
(千米)與其相關的時間![]() (小時)變化的圖像如圖所示.讀圖后填空:
(小時)變化的圖像如圖所示.讀圖后填空:
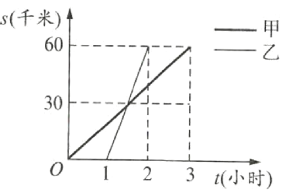
(1)![]() 地與
地與![]() 地之間的距離是______千米;
地之間的距離是______千米;
(2)甲車由![]() 地前往
地前往![]() 地時所對應的
地時所對應的![]() 與
與![]() 的函數(shù)解析式及定義域是__________;
的函數(shù)解析式及定義域是__________;
(3)甲車由![]() 地前往
地前往![]() 地比乙車由
地比乙車由![]() 地前往
地前往![]() 地多用了______小時.
地多用了______小時.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,過格點A、B、C作一圓弧.
(1)弧AC的長為_____(結(jié)果保留π);
(2)點B與圖中格點的連線中,能夠與該圓弧相切的連線所對應的格點的坐標為_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,已知拋物線y=x2+bx+c經(jīng)過A(﹣1,0)、B(3,0)兩點.
(1)求拋物線的解析式和頂點坐標;
(2)當0<x<3時,求y的取值范圍;

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com