
【題目】如圖,在平面直角坐標系中,已知點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,連結
,連結![]() ,拋物線
,拋物線![]() 沿射線
沿射線![]() 方向平移得到拋物線
方向平移得到拋物線![]() ,拋物線
,拋物線![]() 與直線
與直線![]() 交于點
交于點![]() ,設拋物線
,設拋物線![]() 的頂點
的頂點![]() 的橫坐標為
的橫坐標為![]() .
.
(1)求拋物線![]() 的解析式(用含
的解析式(用含![]() 的式子表示);
的式子表示);
(2)連結![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(3)點![]() 為
為![]() 軸上的動點,以
軸上的動點,以![]() 為直角頂點的
為直角頂點的![]() 與
與![]() 相似,求
相似,求![]() 的值.
的值.
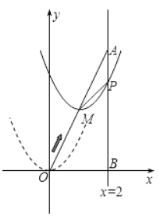
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3) 1或3或4
;(3) 1或3或4
【解析】
(1)先求出OA的解析式,然后根據點M的橫坐標求出縱坐標,即可求出平移的距離,然后利用二次函數圖象的平移規律即可得到拋物線![]() 的解析式;
的解析式;
(2)分兩種情況,點P在A點上方和點P在A點下方,分別畫出相應的圖象,然后分情況討論即可求出m的值,進一步即可求出P點的坐標;
(3)利用相似三角形的性質,分![]() 和
和![]() 兩種情況,然后利用相似三角形的性質進行討論即可得出答案.
兩種情況,然后利用相似三角形的性質進行討論即可得出答案.
(1)設直線OA的解析式為![]() ,
,
將![]() 代入解析式中得
代入解析式中得![]() ,解得
,解得![]() ,
,
∴直線OA解析式為![]() .
.
∵拋物線![]() 的頂點
的頂點![]() 在OA上,且橫坐標為
在OA上,且橫坐標為![]() ,
,
∴![]() ,
,
∴![]() .
.
∵拋物線![]() ,
,
∴拋物線![]() 的解析式為
的解析式為![]() ;
;
(2)∵P點的橫坐標為2,
∴縱坐標為![]() ,
,
![]() .
.
若點P在A點上方,如圖

![]() ,
,
![]() ,
,
∴![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
當![]() 時,
時,![]() ,
,
∴點P的坐標為![]() ;
;
若點P在A點下方,如圖,作線段OD交AB于點D,使![]() ,過點D作OA的垂線交OA的延長線于點N,交OP的延長線于點
,過點D作OA的垂線交OA的延長線于點N,交OP的延長線于點![]() ,
,
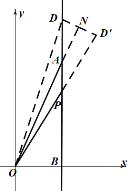
點D的坐標即點P在點A上方時點P的坐標,所以![]() .
.
∵直線OA解析式為![]() ,
,![]() ,
,
∴設直線![]() 的解析式為
的解析式為![]() ,
,
將點D的坐標代入得,![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() .
.
設![]() 的坐標為
的坐標為![]() ,則
,則![]() 且
且![]() ,
,
解得![]() (即點D的坐標),
(即點D的坐標),
∴![]() .
.
設直線![]() 的解析式為
的解析式為![]() ,
,
將![]() 代入解析式中得
代入解析式中得![]() ,解得
,解得![]() ,
,
∴直線![]() 解析式為
解析式為![]() .
.
當![]() 時,
時,![]() ,
,
∴點P的坐標為![]() ,
,
綜上所述,點P的坐標為![]() 或
或![]() ;
;
(3)如圖,若![]() ,則有
,則有![]() ,
,
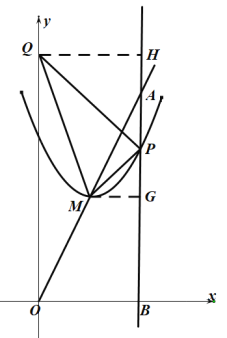
∴![]() .
.
過點M作![]() 交AB于點G,過點Q作
交AB于點G,過點Q作![]() 交AB于點H,
交AB于點H,
∵![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ;
;
同理,若![]() ,解得
,解得![]() 或
或![]() ,
,
當![]() 時,拋物線
時,拋物線![]() 與拋物線
與拋物線![]() 重合,故舍去,
重合,故舍去,
綜上所述,m的值為1或3或4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
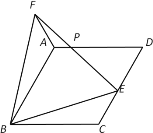
【題目】如圖,在菱形ABCD中,∠ABC=60°,E是CD邊上一點,作等邊△BEF,連接AF.
(1)求證:CE=AF;
(2)EF與AD交于點P,∠DPE=48°,求∠CBE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
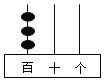
【題目】把3顆算珠放在計數器的3根插棒上構成一個數字,例如,如圖擺放的算珠表示數300.現將3顆算珠任意擺放在這3根插棒上.
(1)若構成的數是兩位數,則十位數字為1的概率為 ;
(2)求構成的數是三位數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
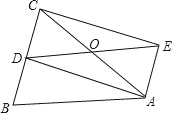
【題目】如圖,在△ABC中,AB=AC,D為BC的中點,四邊形ABDE是平行四邊形.
(1)求證:四邊形ADCE是矩形;
(2)若AC、DE交于點O,四邊形ADCE的面積為16![]() ,CD=4,求∠AOD的度數.
,CD=4,求∠AOD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在不是菱形的平行四邊形![]() 中,
中,![]() 在對角線
在對角線![]() 上,在以下三個條件中再選一個,①
上,在以下三個條件中再選一個,①![]() 分別是
分別是![]() 的中線,②
的中線,②![]() 分別是
分別是![]() 的角平分線,③
的角平分線,③![]() .使得四邊形
.使得四邊形![]() 是平行四邊形,并說明理由.
是平行四邊形,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣x+2與反比例函數y=![]() 的圖象在第二象限內交于點A,過點A作AB⊥x軸于點B,OB=1.
的圖象在第二象限內交于點A,過點A作AB⊥x軸于點B,OB=1.
(1)求該反比例函數的表達式;
(2)若點P是該反比例函數圖象上一點,且△PAB的面積為3,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校積極開展“陽光體育”活動,并開設了跳繩、足球、籃球、跑步四種運動項目,為了解學生最喜愛哪一種項目,隨機抽取了部分學生進行調查,并繪制了如下的條形統計圖和扇形統計圖(部分信息未給出).
(1)求本次被調查的學生人數;
(2)補全條形統計圖;
(3)該校共有3000名學生,請估計全校最喜愛籃球的人數比最喜愛足球的人數多多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是2020年3月26日全國新冠疫情數據表,圖2是3月28日海外各國疫情統計表,圖3是中國和海外的病死率趨勢對比圖,根據這些圖表,選出下列說法中錯誤的一項( )


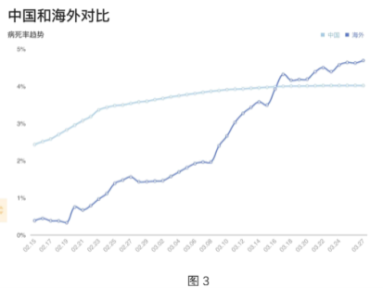
A.圖1顯示每天現有確診數的增加量=累計確診增加量-治愈人數增加量-死亡人數增加量.
B.圖2顯示美國累計確診人數雖然約是德國的兩倍,但每百萬人口的確診人數大約只有德國的一半.
C.圖2顯示意大利當前的治愈率高于西班牙.
D.圖3顯示大約從3月16日開始海外的病死率開始高于中國的病死率
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,BC是⊙O的直徑,A是弦BD延長線上一點,切線DE平分AC于E.

(1)求證:AC是⊙O的切線;
(2)若AD∶DB=3∶2,AC=15,求⊙O的直徑;
(3)在(2)的條件下,求![]() 的值;
的值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com