
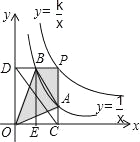
【題目】兩個反比例函數y=![]() (k>1)和y=
(k>1)和y=![]() 在第一象限內的圖象如圖所示,點P在y=
在第一象限內的圖象如圖所示,點P在y=![]() 的圖象上,PC⊥x軸于點C,交y=
的圖象上,PC⊥x軸于點C,交y=![]() 的圖象于點A,PD⊥y軸于點D,交y=
的圖象于點A,PD⊥y軸于點D,交y=![]() 的圖象于點B,BE⊥x軸于點E,當點P在y=
的圖象于點B,BE⊥x軸于點E,當點P在y=![]() 圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化:④△OBA的面積等于四邊形ACEB的面積.其中一定正確的是_____.(填序號)
圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化:④△OBA的面積等于四邊形ACEB的面積.其中一定正確的是_____.(填序號)
【答案】①③④
【解析】
設出點P的坐標,由此可得出A、C、B、D點的坐標,由點的坐標即可表示出各線段的長度,根據線段間的比例關系即可得出BA∥DC,即①成立;找出當PA=PB時,m的值,由此發現②不一定成立;③根據反比例函數系數k的幾何意義可得出三角形OBD、OAC以及矩形OCPD的面積,分割圖形即可得出S四邊形PAOB=k-1,即③成立;根據各邊長度計算出S梯形BECA,結合三角形的面積公式求出S△OBA,發現二者相等,由此得知④成立.綜上即可得出結論.
解:如圖,
①正確.∵A、B在y=![]() 上,
上,
∴S△AOC=S△BOE,
∴![]() OCAC=
OCAC=![]() OEBE,
OEBE,
∴OCAC=OEBE,
∵OC=PD,BE=PC,
∴PDAC=DBPC,
∴![]() ,
,
∴AB∥CD.故此選項正確.
②錯誤,不一定,只有當四邊形OCPD為正方形時滿足PA=PB;
③正確,由于矩形OCPD、△ODB、△OCA的面積為定值,則四邊形PAOB的面積不會發生變化;故此選項正確.
④正確.∵△ODB的面積=△OCA的面積=![]() ,
,
∴△ODB與△OCA的面積相等,同理可得:S△ODB=S△OBE,
∵△OBA的面積=矩形OCPD的面積﹣S△ODB﹣S△BAP﹣S△AOC,四邊形ACEB的面積=矩形OCPD的面積﹣S△ODB﹣S△BAP﹣S△OBE
∴△OBA的面積=四邊形ACEB的面積,故此選項正確,
故一定正確的是①③④.
故答案為:①③④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AE⊥BC于E,將△ABE沿AE所在直線翻折得△AEF,若AB=2,∠B=45°,則△AEF與菱形ABCD重疊部分(陰影部分)的面積為( ).
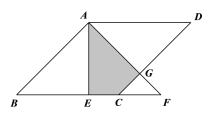
A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 個邊長為
個邊長為![]() 的相鄰正方形的一邊均在同一直線上,點
的相鄰正方形的一邊均在同一直線上,點![]() ,
,![]() ,
,![]() ,…
,…![]() 分別為邊
分別為邊![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的中點,
的中點,![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,…
,…![]() 的面積為
的面積為![]() ,則
,則![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養雞場有2500只雞準備對外出售.從中隨機抽取了一部分雞,根據它們的質量(單位:![]() ),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
),繪制出如下的統計圖①和圖②.請根據相關信息,解答下列問題:
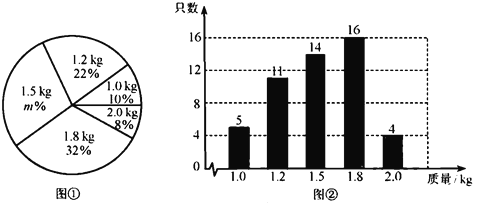
(Ⅰ)圖①中![]() 的值為 ;
的值為 ;
(Ⅱ)求統計的這組數據的平均數、眾數和中位數;
(Ⅲ) 根據樣本數據,估計這2500只雞中,質量為![]() 的約有多少只?
的約有多少只?
查看答案和解析>>
科目:初中數學 來源: 題型:
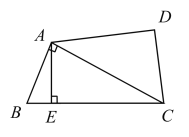
【題目】如圖,小區有一塊四邊形空地![]() ,其中
,其中![]() .為響應沙區創文,美化小區的號召,小區計劃將這塊四邊形空地進行規劃整理.過點
.為響應沙區創文,美化小區的號召,小區計劃將這塊四邊形空地進行規劃整理.過點![]() 作了垂直于
作了垂直于![]() 的小路
的小路![]() .經測量,
.經測量,![]() ,
,![]() ,
,![]() .
.
(1)求這塊空地![]() 的面積;
的面積;
(2)求小路![]() 的長.(答案可含根號)
的長.(答案可含根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩名同學分別進行6次射擊訓練,訓練成績(單位:環)如下表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六交 | |
甲 | 9 | 8 | 6 | 7 | 8 | 10 |
乙 | 8 | 7 | 9 | 7 | 8 | 8 |
對他們的訓練成績作如下分析,其中說法正確的是( )
A. 他們訓練成績的平均數相同 B. 他們訓練成績的中位數不同
C. 他們訓練成績的眾數不同 D. 他們訓練成績的方差不同
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,⊙P的圓心是(2,a)(a >0),半徑是2,與y軸相切于點C,直線y=x被⊙P截得的弦AB的長為![]() ,則a的值是( )
,則a的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com