【題目】如圖，有一個長為24米的籬笆，一面利用墻(墻的最大可用長度為10米)圍成中間隔有一道籬笆的長方形花圃．設花圃的寬AB為x米，面積為S平方米．
(1)求S與x的函數關系式及x的取值范圍；
(2)如果要圍成面積為45平方米的花圃，那么AB的長為多少米？
【答案】(1)S＝－3x2＋24x(
≤x＜8)；（2）5米
【解析】試題分析：
（1）可先用x表示出BC的長，然后根據矩形的面積＝長×寬，得出S與x的函數關系式．根據墻的最大可用長度為10米求出自變量的取值范圍；
（2）根據（1）的函數關系式，將S＝45代入其中，求出x的值即可．
試題解析：
解：（1）由題可知，花圃的寬AB為x米，則BC為（24－3x）米．
這時面積S＝x(24－3x)＝－3x2＋24x．
∵0＜24－3x≤10，
∴
≤x＜8，
即自變量的取值范圍是
≤x＜8；
（2）由條件－3x2＋24x ＝45化為x2－8x＋15＝0，
解得x1＝5，x2＝3，
∵
≤x＜8，
∴x＝3不合題意，舍去，
即花圃的寬AB為5米．
科目：初中數學 來源： 題型：
【題目】如圖，已知鈍角三角形ABC，將△ABC繞點A按逆時針方向旋轉110°得到△AB′C′，連接BB′，若AC′∥BB′，則∠CAB′的度數為( )
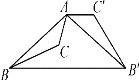
A. 55°B. 65°C. 85°D. 75°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知
、
、
是數軸上三點，點表示的數為3，
，
。
（1）數軸上點表示的數為，點表示的數為。
（2）動點
、
分別從、同時出發，點以每秒2個單位長度的速度沿數軸向右勻速運動，點以每秒1個單位長度的速度沿數軸向左勻速運動，
為
的中點，點
在線段
上，且
，設運動時間為
（
）秒。
①求數軸上、表示的數（用含的式子表示）；
②為何值時，原點
恰好是線段
的中點；
查看答案和解析>>
科目：初中數學 來源： 題型：
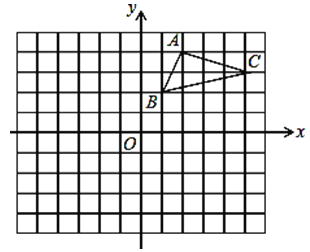
【題目】在平面直角坐標系中，△ABC的三個頂點都在格點上，點A的坐標為（2，4）
（1）畫出△ABC先向左平移1個單位，再向下平移4個單位得到的△A1B1C1，寫出點A1的坐標____________
（2）畫出△A1B1C1繞原點O順時針旋轉90°，得到△A2B2C2，寫出點A2的坐標_______
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖是規格為8×8的正方形網格(小正方形的邊長為1，小正方形的頂點叫格點)，請在所給網格中按下列要求操作：
(1)請在網格中建立平面直角坐標系，使A點坐標為(－2，4)，B點坐標為(－4，2)；
(2)按(1)中的直角坐標系在第二象限內的格點上找點C(C點的橫坐標大于－3)，使點C與線段AB組成一個以AB為底的等腰三角形，則C點坐標是______，△ABC的面積是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法：①倒數等于本身的數是±1；②互為相反數的兩個非零數的商為﹣1；③如果兩個數的絕對值相等，那么這兩個數相等；④有理數可以分為正有理數和負有理數；⑤單項式﹣
的系數是﹣
，次數是6；⑥多項式3πa3+4a2﹣8是三次三項式，其中正確的個數是（ ）
A. 2 個B. 3 個C. 4 個D. 5 個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果一個正整數能表示為兩個連續偶數的平方差，那么稱這個正整數就為“奇巧數，如
，因此
這三個數都是奇巧數。
都是奇巧數嗎？為什么？
設這兩個連續偶數為
（其中
為正整數），由這兩個連續偶數構造的奇巧數是
的倍數嗎？為什么？
研究發現：任意兩個連續“奇巧數”之差是同一個數，請給出驗證。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖在平行四邊形ABCD中，BC=2AB，CE⊥AB于E，F為AD的中點，若∠AEF=54，則∠B=（ ）
A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com