
【題目】如圖,AB∥CD,點E是直線AB上的點,過點E的直線l交直線CD于點F,EG平分∠BEF交CD于點G.在直線l繞點E旋轉的過程中,圖中∠1,∠2的度數可以分別是( )
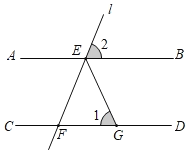
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
【答案】C
【解析】
根據兩直線平行,內錯角相等可得∠BEG,根據角平分線的定義得到∠BEF,根據鄰補角互補求出∠2即可求解.
解:A、∵AB∥CD,
∴∠BEG=∠1=30°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=60°.
∴∠2=180°﹣∠BEF=120°,不符合題意;
B、∵AB∥CD,
∴∠BEG=∠1=56°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=112°.
∴∠2=180°﹣∠BEF=68°,不符合題意;
C、∵AB∥CD,
∴∠BEG=∠1=70°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=140°.
∴∠2=180°﹣∠BEF=40°,符合題意;
D、∵AB∥CD,
∴∠BEG=∠1=100°,
∵EG平分∠BEF,
∴∠BEF=2∠BEG=200°.
∴∠2=360°﹣∠BEF=160°,不符合題意.
故選:C.


 寒假學與練系列答案
寒假學與練系列答案科目:初中數學 來源: 題型:
【題目】如圖,菱形![]() 中,對角線
中,對角線![]() 、
、![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 的速度向點
的速度向點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 支向點
支向點![]() 運動,當其中一個動點停止時另一個動點也隨之停止,設運動時間為
運動,當其中一個動點停止時另一個動點也隨之停止,設運動時間為![]() (單位:
(單位:![]() )(
)(![]() ),以點
),以點![]() 為圓心,
為圓心,![]() 長為半徑的⊙M與射線
長為半徑的⊙M與射線![]() 、線段
、線段![]() 分別交于點
分別交于點![]() 、
、![]() ,連接
,連接![]() .
.
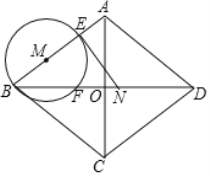
(1)求![]() 的長(用含有
的長(用含有![]() 的代數式表示),并求出
的代數式表示),并求出![]() 的取值范圍;
的取值范圍;
(2)當![]() 為何值時,線段
為何值時,線段![]() 與⊙M相切?
與⊙M相切?
(3)若⊙M與線段![]() 只有一個公共點,求
只有一個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,等邊△ABC,點 E 在 BA 的延長線上,點 D 在 BC 上,且 ED=EC.
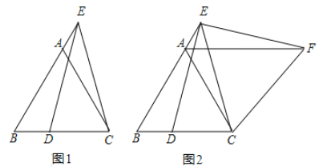
(1)如圖 1,求證:AE=DB;
(2)如圖 2,將△BCE 繞點 C 順時針旋轉 60°至△ACF(點 B、E 的對應點分別為點 A、F),連接 EF.在不添加任何輔助線的情況下,請直接寫出圖中四對線段,使每對線段長度之差等于 AB 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 是
是![]() 邊上一動點,連接
邊上一動點,連接![]() .若
.若![]() 設
設 ![]() (當點
(當點![]() 與點
與點![]() 重合時,
重合時,![]() 的值為
的值為![]() ),
),![]() .
.
小明根據學習函數的經驗,對函數![]() 隨自變量
隨自變量![]() 的變化而變化的規律進行了探究.
的變化而變化的規律進行了探究.
下面是小明的探究過程,請補充完整.
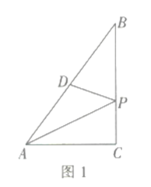
![]() 通過取點、畫圖、計算,得到了
通過取點、畫圖、計算,得到了![]() 與
與![]() 的幾組值,如下表:
的幾組值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
說明:補全表格時,相關數值保留一位小數.
(參考數據:![]() ) .
) .
![]() 如圖2,描出剩余的點,并用光滑的曲線畫出該函數的圖象.
如圖2,描出剩余的點,并用光滑的曲線畫出該函數的圖象.
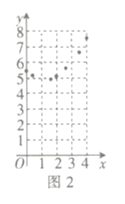
![]() 觀察圖象,下列結論正確的有 _ .
觀察圖象,下列結論正確的有 _ .
①函數有最小值,沒有最大值
②函數有最小值,也有最大值
③當![]() 時,
時,![]() 隨著
隨著![]() 的增大而增大
的增大而增大
④當![]() 時,
時,![]() 隨著
隨著![]() 的增大而減小
的增大而減小
查看答案和解析>>
科目:初中數學 來源: 題型:
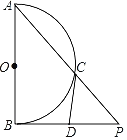
【題目】如圖,已知AB為半圓O的直徑,過點B作PB⊥OB,連接AP交半圓O于點C,D為BP上一點,CD是半圓O的切線.
(1)求證:CD=DP.
(2)已知半圓O的直徑為![]() ,PC=1,求CD的長.
,PC=1,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:⊙O的兩條弦![]() ,
,![]() 相交于點
相交于點![]() ,且
,且![]() .
.
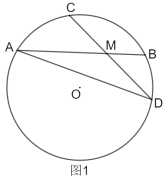
(1)如圖1,連接![]() ,求證:
,求證:![]() .
.
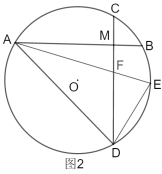
(2)如圖2,在![]() ,在
,在![]() 上取一點
上取一點![]() ,使得
,使得![]() ,
,![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() .
.
①判斷![]() 與
與![]() 是否相等,并說明理由.
是否相等,并說明理由.
②若![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
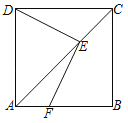
【題目】如圖,正方形ABCD中,AB=3,點E為對角線AC上一點,EF⊥DE交AB于F,若四邊形AFED的面積為4,則四邊形AFED的周長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,CA=8,CB=6,動點P從C出發沿CA方向,以每秒1個單位長度的速度向A點勻速運動,到達A點后立即以原來速度沿AC返回;同時動點Q從點A出發沿AB以每秒1個單位長度向點B勻速運動,當Q到達B時,P、Q兩點同時停止運動.設P、Q運動的時間為t秒(t>0).
(1)當t為何值時,PQ∥CB?
(2)在點P從C向A運動的過程中,在CB上是否存在點E使△CEP與△PQA全等?若存在,求出CE的長;若不存在,請說明理由;
(3)伴隨著P、Q兩點的運動,線段PQ的垂直平分線DF交PQ于點D,交折線QB﹣BC﹣CP于點F.當DF經過點C時,求出t的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com