Question

【題目】在正方形ABCD中，連接BD．

（1）如圖1，AE⊥BD于E．直接寫出∠BAE的度數．

（2）如圖1，在（1）的條件下，將△AEB以A旋轉中心，沿逆時針方向旋轉30°后得到△AB′E′，AB′與BD交于M，AE′的延長線與BD交于N．

①依題意補全圖1；

②用等式表示線段BM、DN和MN之間的數量關系，并證明．

（3）如圖2，E、F是邊BC、CD上的點，△CEF周長是正方形ABCD周長的一半，AE、AF分別與BD交于M、N，寫出判斷線段BM、DN、MN之間數量關系的思路．（不必寫出完整推理過程）

Answer 1

【答案】（1）∠BAE的度數為45°；（2）①補全圖見解析；②BM、DN和MN之間的數量關系是BM2+MD2=MN2，理由見解析；（3）思路見解析.

【解析】（1）利用等腰直角三角形的性質即可；

（2）依題意畫出如圖1所示的圖形，根據性質和正方形的性質，判斷線段的關系，再利用勾股定理得到FB2+BM2=FM2，再判斷出FM=MN即可；

（3）利用△CEF周長是正方形ABCD周長的一半，判斷出EF=EG，再利用（2）證明即可．

解：（1）∵BD是正方形ABCD的對角線，∴∠ABD=∠ADB=45°，

∵AE⊥BD，∴∠ABE=∠BAE=45°，

（2）①依題意補全圖形，如圖1所示，

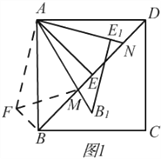
②BM、DN和MN之間的數量關系是BM2+MD2=MN2，

將△AND繞點D順時針旋轉90°，得到△AFB，

∴∠ADB=∠FBA，∠BAF=∠DAN，DN=BF，AF=AN，

∵在正方形ABCD中，AE⊥BD，∴∠ADB=∠ABD=45°，

∴∠FBM=∠FBA+∠ABD=∠ADB+∠ABD=90°，

在Rt△BFM中，根據勾股定理得，FB2+BM2=FM2，

∵旋轉△ANE得到AB1E1，∴∠E1AB1=45°，∴∠BAB1+∠DAN=90°﹣45°=45°，

∵∠BAF=DAN，∴∠BAB1+∠BAF=45°，∴∠FAM=45°，∴∠FAM=∠E1AB1，

∵AM=AM，AF=AN，∴△AFM≌△ANM，∴FM=MN，

∵FB2+BM2=FM2，∴DN2+BM2=MN2，

（3）如圖2，

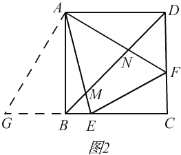
將△ADF繞點A順時針旋轉90°得到△ABG，∴DF=GB，

∵正方形ABCD的周長為4AB，△CEF周長為EF+EC+CF，

∵△CEF周長是正方形ABCD周長的一半，∴4AB=2（EF+EC+CF），∴2AB=EF+EC+CF

∵EC=AB﹣BE，CF=AB﹣DF，∴2AB=EF+AB﹣BE+AB﹣DF，∴EF=DF+BE，

∵DF=GB，∴EF=GB+BE=GE，由旋轉得到AD=AG=AB，

∵AM=AM，∴△AEG≌△AEF，∠EAG=∠EAF=45°，和（2）的②一樣，得到DN2+BM2=MN2．

“點睛”此題是四邊形綜合題，主要考查了正方形的性質、旋轉的性質，三角形的全等，判斷出（△AFN≌△ANM，得到FM=MM），是解題的關鍵.