
【題目】已知:如圖1,直線y= ![]() x+6與x軸、y軸分別交于點A、C兩點,點B的橫坐標為2.
x+6與x軸、y軸分別交于點A、C兩點,點B的橫坐標為2. 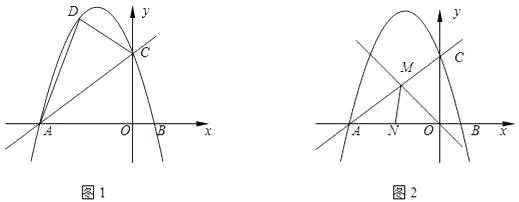
(1)求A、C兩點的坐標和拋物線的函數關系式;
(2)點D是直線AC上方拋物線上任意一點,P為線段AC上一點,且S△PCD=2S△PAD , 求點P的坐標;
(3)如圖2,另有一條直線y=﹣x與直線AC交于點M,N為線段OA上一點,∠AMN=∠AOM.點Q為x軸負半軸上一點,且點Q到直線MN和直線MO的距離相等,求點Q的坐標.
【答案】
(1)解:在y= ![]() x+6中,
x+6中,
令x=0,則y=6;令y=0,則x=﹣8,
∴A(﹣8,0),C(0,6),
∵點B的橫坐標為2,
∴B(2,0),
設拋物線解析式為y=a(x+8)(x﹣2),則
把C(0,6)代入,得6=a×(﹣16),
∴a=﹣ ![]() ,
,
∴y=﹣ ![]() (x+8)(x﹣2),
(x+8)(x﹣2),
即 ![]()
(2)解:如圖所示,過P作PH⊥AO于H,
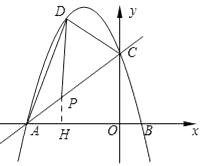
∵S△PCD=2S△PAD,
∴AP:PC=1:2,
∵PH∥CO,
∴AH:HO=1:2,
即OH= ![]() AO,
AO,
又∵AO=8,
∴OH=8× ![]() =
= ![]() ,
,
∴點P的橫坐標為 ![]() ,
,
在直線y= ![]() x+6中,當x=
x+6中,當x= ![]() 時,y=
時,y= ![]() ×(
×( ![]() )+6=2,
)+6=2,
∴點P的縱坐標為2,
∴點P的坐標為( ![]() ,2)
,2)
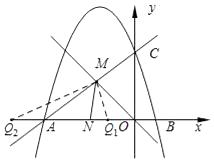
(3)解:分兩種情況:
①當點Q1為∠NMO的平分線與x軸的交點時,點Q1到直線MN和直線MO的距離相等,
∵直線y=﹣x與直線y= ![]() x+6交于點M,
x+6交于點M,
∴M(﹣ ![]() ,
, ![]() ),
),
又∵A(﹣8,0),
∴由兩點間距離公式可得AM= ![]() =
= ![]() ,
,
∵∠AMN=∠AOM,∠MAN=∠OAM,
∴△AMN∽△AOM,
∴AM2=AN×AO,即( ![]() )2=AN×8,
)2=AN×8,
∴AN= ![]() ,
,
∴ON=AO﹣AN= ![]() ,
,
即N(﹣ ![]() ,0),
,0),
∴由兩點間距離公式可得MN= ![]() ,MO=
,MO= ![]() ,
,
∵MQ1平分∠NMO,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴OQ1= ![]() NO=
NO= ![]() =
= ![]() ,
,
即點Q1的坐標為( ![]() ,0);
,0);
②當點Q2為∠NMO的鄰補角的平分線與x軸的交點時,點Q2到直線MN和直線MO的距離相等,
根據Q1( ![]() ,0),M(﹣
,0),M(﹣ ![]() ,
, ![]() ),可得
),可得
直線MQ1解析式為y=﹣3x﹣ ![]() ,
,
∵MQ1⊥MQ2,
∴可設直線MQ2解析式為y= ![]() x+b,
x+b,
把M(﹣ ![]() ,
, ![]() )代入,可得b=
)代入,可得b= ![]() ,
,
∴直線MQ2解析式為y= ![]() x+
x+ ![]() ,
,
∴當y=0時,0= ![]() x+
x+ ![]() ,
,
解得x=﹣ ![]() ,
,
即點Q2的坐標為( ![]() ,0).
,0).
綜上所述,點Q的坐標為( ![]() ,0)或(
,0)或( ![]() ,0)
,0)
【解析】(1)根據直線y= ![]() x+6,可得A(﹣8,0),C(0,6),設拋物線解析式為y=a(x+8)(x﹣2),把C(0,6)代入,可得拋物線的函數關系式;(2)過P作PH⊥AO于H,根據S△PCD=2S△PAD , 可得AP:PC=1:2,即AH:HO=1:2,進而得到OH=
x+6,可得A(﹣8,0),C(0,6),設拋物線解析式為y=a(x+8)(x﹣2),把C(0,6)代入,可得拋物線的函數關系式;(2)過P作PH⊥AO于H,根據S△PCD=2S△PAD , 可得AP:PC=1:2,即AH:HO=1:2,進而得到OH= ![]() AO=8×
AO=8× ![]() =
= ![]() ,在直線y=
,在直線y= ![]() x+6中,當x=
x+6中,當x= ![]() 時,y=
時,y= ![]() ×(
×( ![]() )+6=2,可得點P的坐標為(
)+6=2,可得點P的坐標為( ![]() ,2);(3)分兩種情況進行討論:①當點Q1為∠NMO的平分線與x軸的交點時,點Q1到直線MN和直線MO的距離相等;②當點Q2為∠NMO的鄰補角的平分線與x軸的交點時,點Q2到直線MN和直線MO的距離相等,根據相似三角形的性質求得N(﹣
,2);(3)分兩種情況進行討論:①當點Q1為∠NMO的平分線與x軸的交點時,點Q1到直線MN和直線MO的距離相等;②當點Q2為∠NMO的鄰補角的平分線與x軸的交點時,點Q2到直線MN和直線MO的距離相等,根據相似三角形的性質求得N(﹣ ![]() ,0),再根據角平分線的性質可得點Q1的坐標為(
,0),再根據角平分線的性質可得點Q1的坐標為( ![]() ,0);最后根據MQ1⊥MQ2 , 可得直線MQ2解析式為y=
,0);最后根據MQ1⊥MQ2 , 可得直線MQ2解析式為y= ![]() x+
x+ ![]() ,進而得到點Q2的坐標為(
,進而得到點Q2的坐標為( ![]() ,0).
,0).
【考點精析】通過靈活運用角平分線的性質定理和相似三角形的判定與性質,掌握定理1:在角的平分線上的點到這個角的兩邊的距離相等; 定理2:一個角的兩邊的距離相等的點,在這個角的平分線上;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方即可以解答此題.


科目:初中數學 來源: 題型:
【題目】生活經驗表明,靠墻擺放的梯子,當50°≤α≤70°時(α為梯子與地面所成的角),能夠使人安全攀爬.現在有一長為6米的梯子AB,試求能夠使人安全攀爬時,梯子的頂端能達到的最大高度AC.
(結果保留兩個有效數字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)觀察發現
![]() ,
,![]() ,
,![]() ,……,
,……,![]() .
.
![]() =1﹣
=1﹣![]() =
=![]() .
.
![]() =1﹣
=1﹣![]() =
=![]() .
.
![]() = .
= .
(2)構建模型
![]() = .(n為正整數)
= .(n為正整數)
(3)拓展應用:
①![]() = .
= .
②![]() = .
= .
③一個數的八分之一,二十四分之一,四十八分之一,八十分之一的和比這個數的四分之一小1,求這個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,從A地到B地的公路需經過C地,圖中AC=10千米,∠CAB=25°,∠CBA=37°,因城市規劃的需要,將在A、B兩地之間修建一條筆直的公路. 
(1)求改直的公路AB的長;
(2)問公路改直后比原來縮短了多少千米?(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C為⊙O上一點,AD⊥CD,(點D在⊙O外)AC平分∠BAD. 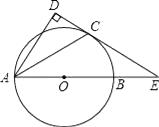
(1)求證:CD是⊙O的切線;
(2)若DC、AB的延長線相交于點E,且DE=12,AD=9,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC的內切圓⊙O與兩直角邊AB,BC分別相切于點D,E,過劣弧 ![]() (不包括端點D,E)上任一點P作⊙O的切線MN與AB,BC分別交于點M,N,若⊙O的半徑為r,則Rt△MBN的周長為( )
(不包括端點D,E)上任一點P作⊙O的切線MN與AB,BC分別交于點M,N,若⊙O的半徑為r,則Rt△MBN的周長為( ) 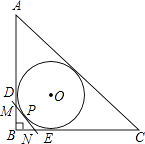
A.r
B.![]() ?r
?r
C.2r
D.![]() ?r
?r
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等腰△ABC的頂角∠A=36°(如圖). 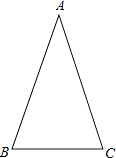
(1)作底角∠ABC的平分線BD,交AC于點D(用尺規作圖,不寫作法,但保留作圖痕跡,然后用墨水筆加墨);
(2)通過計算說明△ABD和△BDC都是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A、B、C、D、E在同一直線上,且AC=BD,E是線段BC的中點.
![]()
(1)點E是線段AD的中點嗎?說明理由;
(2)當AD=10,AB=3時,求線段BE的長度.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com