
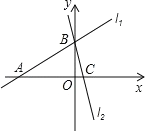
【題目】如圖,直線y1=-2x+3和直線y2=mx-3分別交y軸于點A、B ,兩直線交于點C(1,n).
(1)求 m、n 的值;
(2)求△ABC的面積;
(3)請根據圖象直接寫出:當 y1<y2時,自變量 x 的取值范圍.
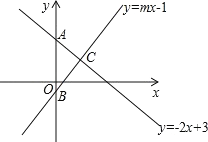
【答案】(1)m=4;(2)3;(3)當 x>1 時,y1<y2.
【解析】
(1)先把C(1,n)代入y1=-2x+3可求出n的值,從而確定C點坐標,然后把C點坐標代入入y2=mx-3即可求出m的值;
(2)先確定A點和B點坐標,然后根據三角形面積公式求解;
(3)觀察函數圖象得到當x>1時,直線y2=mx-3都在直線y1=-2x+3的上方.
(1)把 C(1,n)代入 y1=﹣2x+3 得 n=﹣2+3=1, 所以 C 點坐標為(1,1),
把 C(1,1)代入 y2=mx﹣3 得 m﹣3=1,解得 m=4;
(2)當 x=0 時,y=﹣2x+3=3,則 A(0,3); 當 x=0 時,y=4x﹣3=﹣3,則 B(0,﹣3),
所以△ABC 的面積=![]() ×(3+3)×1=3;
×(3+3)×1=3;
(3)當 x>1 時,y1<y2.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,第一個正方形ABCD的位置如圖所示,點A的坐標為(2,0),點D的坐標為(0,4),延長CB交x軸于點A1,作第二個正方形A1B1C1C;延長C1B1交x軸于點A2,作第三個正方形A2B2C2C1…按這樣的規律進行下去,第2018個正方形的面積為( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四邊形ADEF是正方形,點B、C分別在邊AD、AF上,此時BD=CF,BD⊥CF成立.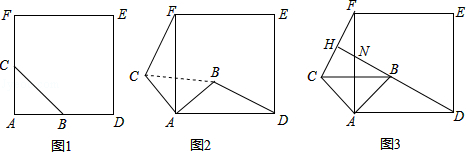
(1)當△ABC繞點A逆時針旋轉θ(0°<θ<90°)時,如圖2,BD=CF成立嗎?若成立,請證明,若不成立,請說明理由;
(2)當△ABC繞點A逆時針旋轉45°時,如圖3,延長BD交CF于點H.
①求證:BD⊥CF;
②當AB=2,AD=3 ![]() 時,求線段DH的長.
時,求線段DH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
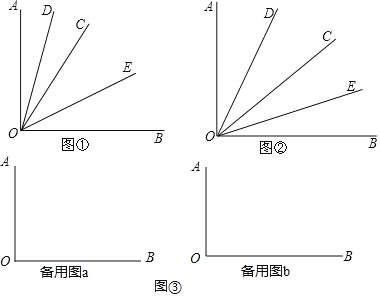
【題目】已知:∠AOB是一個直角,作射線OC,再分別作∠AOC和∠BOC的平分線OD、OE.
(1)如圖①,當∠BOC=70°時,求∠DOE的度數;
(2)如圖②,若射線OC在∠AOB內部繞O點旋轉,當∠BOC=α時,求∠DOE的度數.
(3)如圖③,當射線OC在∠AOB外繞O點旋轉時,畫出圖形,直接寫出∠DOE的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,lA,lB分別表示A步行與B騎車在同一路上行駛的路程S與時間t的關系.
(1)B出發時與A相距______千米.
(2)B走了一段路后,自行車發生故障,進行修理,所用的時間是______小時.
(3)B出發后______小時與A相遇.
(4)若B的自行車不發生故障,保持出發時的速度前進,______小時與A相遇,相遇點離B的出發點______千米.在圖中表示出這個相遇點C.
(5)求出A行走的路程S與時間t的函數關系式。

查看答案和解析>>
科目:初中數學 來源: 題型:
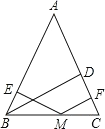
【題目】大家在學完勾股定理的證明后發現運用“同一圖形的面積不同表示方式相同”可 以證明一類含有線段的等式,這種解決問題的方法我們稱之為面積法.學有所用:在等腰 三角形 ABC中,AB=AC,其一腰上的高為h,M 是底邊BC上的任意一點,M 到腰AB、AC 的距離分別為 h1、h2 .
(1)請你結合圖形來證明: h1+h2=h;
(2)當點M在BC延長線上時,h1、h2、h 之間又有什么樣的結論.請你畫出圖形,并直
接寫出結論不必證明;
(3)利用以上結論解答,如圖在平面直角坐標系中有兩條直線l1:y=x+3,l2:y=-3x+3
若 l2上的一點M 到l1的距離是![]() ,求點 M 的坐標.
,求點 M 的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:一列數x1,x2,x3,……,xn,從這列數的第二項數起,每一項與它前面的項的比都等于一個常數,就把這樣的一列數叫做等比數列,這個常數叫做等比數列的公比.如1,2,4,8,…….這列數就是等比數列,公比是2.
(1)等比數列5,-15,45,-135,……,請計算這個等比數列的公比?
(2)若一個等比數列:-9,a,b,……,的公比是-![]() ,求a,b的值.
,求a,b的值.
(3)一個等比數列的第二項是-10,第三項是-20,求這組數列的第一項和第五項.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC=60°,AB=2,點P是這個菱形內部或邊上的一點,若以點P、B、C為頂點的三角形是等腰三角形,則P、D(P、D兩點不重合)兩點間的最短距離為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從甲地到乙地,先是一段平路,然后是一段上坡路。小明騎車從甲地出發,到達乙地后立即原路返回甲地,途中休息了一段時間。假設小明騎車在平路、上坡、下坡時分別保持勻速前進.已知小明騎車上坡的速度比平路上的速度每小時少5km,下坡的速度比在平路上的速度每小時多5km。設小明出發xh后,到達離甲地y km的地方,圖中的折線OABCDE表示y與x之間的函數關系.
(1)小明騎車在平路上的速度為 km/h;他途中休息了 h;
(2)求線段AB,BC所表示的y與![]() 之間的函數關系式;
之間的函數關系式;
(3)如果小明兩次經過途中某一地點的時間間隔為0.15h,那么該地點離甲地多遠?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com