
【題目】如圖,在菱形ABCD中,CE⊥AB交AB延長線于點E,點F為點B關于CE的對稱點,連接CF,分別延長DC,CF至點G,H,使FH=CG,連接AG,DH交于點P.
(1)依題意補全圖1;
(2)猜想AG和DH的數量關系并證明;
(3)若∠DAB=70°,是否存在點G,使得△ADP為等邊三角形?若存在,求出CG的長;若不存在,說明理由.


【答案】(1)見解析;(2) AG=DH,理由見解析;(3) 不存在.理由見解析.
【解析】(1)依題意畫圖;
(2)根據菱形性質得![]() ,
,![]() ∥
∥![]() ,
,![]() ;由點
;由點![]() 為點
為點![]() 關于
關于![]() 的對稱點,得
的對稱點,得![]() 垂直平分
垂直平分![]() ,故
,故![]() ,
,![]() ,所以
,所以![]() ,再證
,再證![]() ,
,
由![]() ,
,![]() ,得
,得![]() .可證△
.可證△![]() ≌△
≌△![]() .
.
(3)由(2)可知,∠DAG=∠CDH,∠G=∠GAB,
證得∠DPA=∠PDG+∠G=∠DAG+∠GAB=70°>60°,故△ADP不可能是等邊三角形.
(1)補全的圖形,如圖所示.
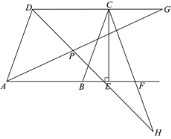
(2)AG=DH.
證明:∵四邊形ABCD是菱形,
∴![]() ,
,![]() ∥
∥![]() ,
,![]() .
.
∵點![]() 為點
為點![]() 關于
關于![]() 的對稱點,
的對稱點,
∴![]() 垂直平分
垂直平分![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴△![]() ≌△
≌△![]() .
.
∴![]() .
.
(3)不存在.
理由如下:
由(2)可知,∠DAG=∠CDH,∠G=∠GAB,
∴∠DPA=∠PDG+∠G=∠DAG+∠GAB=70°>60°.
∴△ADP不可能是等邊三角形.


科目:初中數學 來源: 題型:
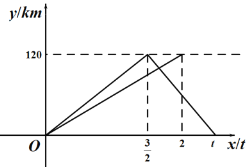
【題目】一輛轎車從甲地駛往乙地,到達乙地后立即返回甲地,速度是原來的1.5倍,往返共用t小時.一輛貨車同時從甲地駛往乙地,到達乙地后停止.兩車同時出發,勻速行駛,設轎車行駛的時間為x(h),兩車離開甲地的距離為y(km),兩車行駛過程中y與x之間的函數圖象如圖所示.
(1)轎車從乙地返回甲地的速度為 km/t,t= h;
(2)求轎車從乙地返回甲地時y與x之間的函數關系式;
(3)當轎車從甲地返回乙地的途中與貨車相遇時,求相遇處到甲地的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
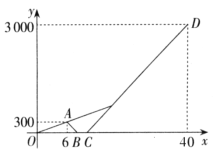
【題目】為營造書香家庭,周末小亮和姐姐一起從家出發去圖書館借書,走了6min發現忘帶借書證,小亮立即騎路邊共享單車返回家中取借書證,姐姐以原來的速度繼續向前走,小亮取回借書證后騎單車原路原速前往圖書館,小亮追上姐姐后用單車帶著姐姐一起前往圖書館。已知騎車的速度是步行速度的2倍,如圖是小亮和姐姐距離家的路程y(m)與出發的時間x(min)的函數圖象,根據圖象解答下列問題:
(1)小亮在家停留了多長時間?
(2)求小亮騎車從家出發去圖書館時距家的路程 y(m)與出發時間 x(min)之間的函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線![]() 的表達式為
的表達式為![]() ,點A,B的坐標分別為
,點A,B的坐標分別為
(1,0),(0,2),直線AB與直線![]() 相交于點P.
相交于點P.
(1)求直線AB的表達式;
(2)求點P的坐標;
(3)若直線![]() 上存在一點C,使得△APC的面積是△APO的面積的2倍,直接寫出點C的坐標.
上存在一點C,使得△APC的面積是△APO的面積的2倍,直接寫出點C的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一束光線與水平面成60°的角度照射地面,現在地面AB上支放一個平面鏡CD,使這束光線經過平面鏡反射后成水平光線,則平面鏡CD與地面AB所成角∠DCB的度數等于( ) 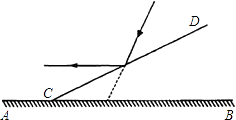
A.30°
B.45°
C.50°
D.60°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=--![]() x+8與x軸,y軸分別交于點A,點B,點D在y軸的負半軸上,若將△DAB沿直線AD折疊,點B恰好落在x軸正半軸上的點C處.
x+8與x軸,y軸分別交于點A,點B,點D在y軸的負半軸上,若將△DAB沿直線AD折疊,點B恰好落在x軸正半軸上的點C處.
(1)求AB的長和點C的坐標;
(2)求直線CD的表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點.
(1)求證:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】國家規定,“中小學生每天在校體育鍛煉時間不小于1小時”,某地區就“每天在校體育鍛煉時間”的問題隨機調查了若干名中學生,根據調查結果制作如下統計圖(不完整).其中分組情況:A組:時間小于0.5小時;B組:時間大于等于0.5小時且小于1小時;C組:時間大于等于1小時且小于1.5小時;D組:時間大于等于1.5小時.
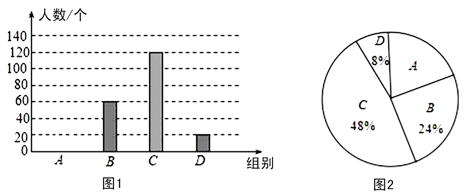
根據以上信息,回答下列問題:
(1)A組的人數是 人,并補全條形統計圖;
(2)本次調查數據的中位數落在組 ;
(3)根據統計數據估計該地區25 000名中學生中,達到國家規定的每天在校體育鍛煉時間的人數約有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在大樓AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小紅在斜坡下的點C處測得樓頂B的仰角為60°,在斜坡上的點D處測得樓頂B的仰角為45°,其中點A、C、E在同一直線上.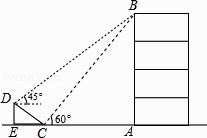
(1)求斜坡CD的高度DE;
(2)求大樓AB的高度(結果保留根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com