
【題目】如圖,在直角坐標系中點A(2,0),點P在射線 ![]() (x<0)上運動,設點P的橫坐標為a,以AP為直徑作⊙C,連接OP、PB,過點P作PQ⊥OP交⊙C于點Q.
(x<0)上運動,設點P的橫坐標為a,以AP為直徑作⊙C,連接OP、PB,過點P作PQ⊥OP交⊙C于點Q.
(1)證明:∠AOP=∠BPQ;
(2)當點P在運動的過程中,線段PQ的長度是否發生變化,若變化,請用含a的代數式表示PQ的長;若不變,求出PQ的長;
(3)當tan∠APO= ![]() 時,①求點Q坐標;②點D是圓上任意一點,求QD+
時,①求點Q坐標;②點D是圓上任意一點,求QD+ ![]() OD的最小值.
OD的最小值.
【答案】
(1)解:由題意得點P(a,- ![]() a),∵AP為直徑,∴∠PBA=90°,∴tan∠BOP=
a),∵AP為直徑,∴∠PBA=90°,∴tan∠BOP= ![]() ,∴∠BPO=30°,∠POB=60°,∵PQ⊥OP,∴∠BPQ=∠AOP=120°
,∴∠BPO=30°,∠POB=60°,∵PQ⊥OP,∴∠BPQ=∠AOP=120°
(2)解:不變.如圖1,連結BQ,
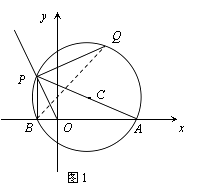
∵∠Q=∠PAO,∠BPQ=∠AOP,
∴△BPQ∽△POA.
∴ ![]() ,
,
∴PQ= ![]()
(3)解:①如圖2,連結AQ,過點Q作QH⊥BP
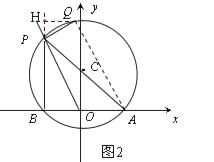
∵AP是直徑,
∴∠PQA=90°.
∵∠OPQ=90°,
∴OP∥AQ.
∴∠OPA=∠PAQ,
∵tan∠OPA= ![]() ,
,
∴ ![]() ,
,
∵PQ= ![]() ,
,
∴AQ=5,AP=2 ![]() ,在RT△ABP中,AB=2-a,BP=-
,在RT△ABP中,AB=2-a,BP=- ![]() a,由(2-a)2+(
a,由(2-a)2+( ![]() a)2=(2
a)2=(2 ![]() )2,解得a1=-2,a2=3(舍去),
)2,解得a1=-2,a2=3(舍去),
∴P(-2,2 ![]() ),∠BPQ=120°,
),∠BPQ=120°,
∴∠HPQ=60°,
∴PH= ![]() ,HQ=
,HQ= ![]() ,
,
∴點Q(- ![]() ,
, ![]() );
);
②如圖3,
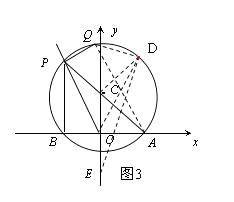
由①得CD= ![]() ,
,
∵P(-2,2 ![]() ),A(2,0),
),A(2,0),
∴C(0, ![]() ) ,OC=
) ,OC= ![]() ,在y軸上找點E使CE=
,在y軸上找點E使CE= ![]() ,
,
∴E(0,- ![]() ),
),
∴CD2=CO·CE,
∵∠DCO=∠ECD,
∴△DCO∽△ECD,
∴DE= ![]() OD,
OD,
∵QD+DE≥QE,
∴QD+ ![]() OD的最小值為
OD的最小值為 ![]()
【解析】(1)首先表示出P點的坐標,根據直徑所對的圓周角是直角得出∠PBA=90°,根據正切三角函數的定義及特殊銳角三角函數值得出∠POB=60°,根據三角形的內角和得出∠BPO=30°,再根據垂直的定義得出∠BPQ=∠AOP=120°;
(2)不變.如圖1,連結BQ,根據同弧所對的圓周角相等得出∠Q=∠PAO,又由(1)知∠BPQ=∠AOP,從而判斷出△BPQ∽△POA,根據相似三角形對應邊成比例得出答案;
(3)①如圖2,連結AQ,過點Q作QH⊥BP,根據直徑所對的圓周角是直角得出∠PQA=90°,然后根據同旁內角互補兩直線平行得出OP∥AQ,根據平行線的性質得出∠OPA=∠PAQ,然后根據正切三角函數的定義打得出![]() =
=![]() ,從而得出AQ,AP的長,在Rt△ABP中,根據勾股定理得出關于a的方程,求出a的值,從而得出p點的坐標,進一步得出Q點的坐標;②如圖3,由①得CD=
,從而得出AQ,AP的長,在Rt△ABP中,根據勾股定理得出關于a的方程,求出a的值,從而得出p點的坐標,進一步得出Q點的坐標;②如圖3,由①得CD= ![]() ,由P,A兩點的坐標得出C點的坐標及OC的長,在y軸上找點E使CE=
,由P,A兩點的坐標得出C點的坐標及OC的長,在y軸上找點E使CE= ![]() ,進而得出E點坐標,從而得出CD2=CO·CE,然后判斷出△DCO∽△ECD,根據相似三角形的性質得出DE=
,進而得出E點坐標,從而得出CD2=CO·CE,然后判斷出△DCO∽△ECD,根據相似三角形的性質得出DE= ![]() OD,又因QD+DE≥QE,從而得出答案。
OD,又因QD+DE≥QE,從而得出答案。
【考點精析】認真審題,首先需要了解平行線的判定與性質(由角的相等或互補(數量關系)的條件,得到兩條直線平行(位置關系)這是平行線的判定;由平行線(位置關系)得到有關角相等或互補(數量關系)的結論是平行線的性質),還要掌握圓周角定理(頂點在圓心上的角叫做圓心角;頂點在圓周上,且它的兩邊分別與圓有另一個交點的角叫做圓周角;一條弧所對的圓周角等于它所對的圓心角的一半)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】如果三個數a、b、c滿足其中一個數的兩倍等于另外兩個數的和,我們稱這三個數a、b、c是“等差數”若正比例函數y=2x的圖象上有三點A(![]() m﹣1,y1)、B(m,y2)、C(2m+1,y3),且這三點的縱坐標y1、y2、y3是“等差數”,則m=_____.
m﹣1,y1)、B(m,y2)、C(2m+1,y3),且這三點的縱坐標y1、y2、y3是“等差數”,則m=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算下列各題:
(1)(﹣x2+3y)(﹣2xy)
(2)[5xy2(x2﹣3xy)+(3x2y2)3]÷(5xy)2
(3)(﹣4x﹣3y2)(3y2﹣4x)
(4)(a+b)(a2﹣ab+b2)
(5)a(a﹣b)2﹣2b(a﹣b)(a+b)
(6)10002﹣998×1002(簡便運算).
(7)(3a2+![]() )(3a2﹣
)(3a2﹣![]() b)(9a4﹣
b)(9a4﹣![]() b2)
b2)
(8)(a2﹣ab+b2)(a2+ab+b2).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】聰聰是一位非常喜歡動腦筋的初一學生,特別是學了幾何后,更覺得數學奇妙,當聰聰學完![]() 圖形的初步知識
圖形的初步知識![]() 后對角平分線興趣更濃厚,下面請你和聰聰同學一起來探究奇妙的角平分線吧
后對角平分線興趣更濃厚,下面請你和聰聰同學一起來探究奇妙的角平分線吧![]() 已知
已知![]() ,射線OE,OF分別是
,射線OE,OF分別是![]() 和
和![]() 的角平分線.
的角平分線.
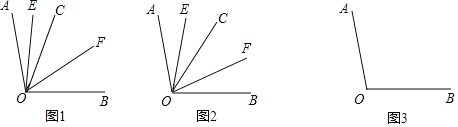
![]() 如圖1,若射線OC在
如圖1,若射線OC在![]() 的內部,且
的內部,且![]() ,求
,求![]() 的度數;
的度數;
![]() 如圖2,若射線OC在
如圖2,若射線OC在![]() 的內部繞點O旋轉,且
的內部繞點O旋轉,且![]() ,求
,求![]() 的度數;
的度數;
![]() 若射線OC在
若射線OC在![]() 的外部繞點O旋轉
的外部繞點O旋轉![]() 旋轉中
旋轉中![]() ,
,![]() 均指小于
均指小于![]() 的角
的角![]() ,其余條件不變,請借助圖3探究
,其余條件不變,請借助圖3探究![]() 的大小,請直接寫出
的大小,請直接寫出![]() 的度數
的度數![]() 不寫探究過程
不寫探究過程![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分線與AB的中垂線交于點O,點C沿EF折疊后與點O重合,則∠CEO的度數是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知數軸上有兩點A、B,點A對應的數是40,點B對應的數是![]() .
.
![]() 求線段AB的長.
求線段AB的長.
![]() 如圖2,O表示原點,動點P、T分別從B、O兩點同時出發向左運動,同時動點Q從點A出發向右運動,點P、T、Q的速度分別為5個單位長度
如圖2,O表示原點,動點P、T分別從B、O兩點同時出發向左運動,同時動點Q從點A出發向右運動,點P、T、Q的速度分別為5個單位長度![]() 秒、1個單位長度
秒、1個單位長度![]() 秒、2個單位長度
秒、2個單位長度![]() 秒,設運動時間為t.
秒,設運動時間為t.
![]() 求點P、T、Q表示的數
求點P、T、Q表示的數![]() 用含有t的代數式表示
用含有t的代數式表示![]() ;
;
![]() 在運動過程中,如果點M為線段PT的中點,點N為線段OQ的中點,試說明在運動過程中等量關系
在運動過程中,如果點M為線段PT的中點,點N為線段OQ的中點,試說明在運動過程中等量關系![]() 始終成立.
始終成立.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小李在某商場購買![]() 兩種商品若干次(每次
兩種商品若干次(每次![]() 商品都買) ,其中前兩次均按標價購買,第三次購買時,
商品都買) ,其中前兩次均按標價購買,第三次購買時,![]() 商品同時打折.三次購買
商品同時打折.三次購買![]() 商品的數量和費用如下表所示:
商品的數量和費用如下表所示:
購買A商品的數量/個 | 購買B商品的數量/個 | 購買總費用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的標價各是多少元?
商品的標價各是多少元?
(2)若小李第三次購買時![]() 商品的折扣相同,則商場是打幾折出售這兩種商品的?
商品的折扣相同,則商場是打幾折出售這兩種商品的?
(3)在(2)的條件下,若小李第四次購買![]() 商品共花去了
商品共花去了![]() 元,則小李的購買方案可能有哪幾種?
元,則小李的購買方案可能有哪幾種?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC=60°,AB=1,E為BC的中點,則對角線BD上的動點P到E、C兩點的距離之和的最小值為( )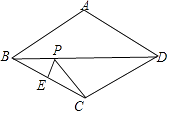
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com