
【題目】已知點A(﹣1,1)、B(4,6)在拋物線y=ax2+bx上
(1)求拋物線的解析式;
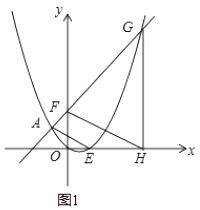
(2)如圖1,點F的坐標為(0,m)(m>2),直線AF交拋物線于另一點G,過點G作x軸的垂線,垂足為H.設拋物線與x軸的正半軸交于點E,連接FH、AE,求證:FH∥AE;
(3)如圖2,直線AB分別交x軸、y軸于C、D兩點.點P從點C出發,沿射線CD方向勻速運動,速度為每秒 ![]()
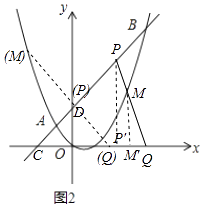
個單位長度;同時點Q從原點O出發,沿x軸正方向勻速運動,速度為每秒1個單位長度.點M是直線PQ與拋物線的一個交點,當運動到t秒時,QM=2PM,直接寫出t的值.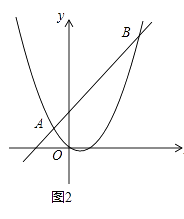
【答案】
(1)解:將點A(﹣1,1)、B(4,6)代入y=ax2+bx中,
![]() ,解得:
,解得:  ,
,
∴拋物線的解析式為y= ![]() x2﹣
x2﹣ ![]() x.
x.
(2)證明:設直線AF的解析式為y=kx+m,
將點A(﹣1,1)代入y=kx+m中,即﹣k+m=1,
∴k=m﹣1,
∴直線AF的解析式為y=(m﹣1)x+m.
聯立直線AF和拋物線解析式成方程組,
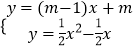 ,解得:
,解得: ![]() ,
, ![]() ,
,
∴點G的坐標為(2m,2m2﹣m).
∵GH⊥x軸,
∴點H的坐標為(2m,0).
∵拋物線的解析式為y= ![]() x2﹣
x2﹣ ![]() x=
x= ![]() x(x﹣1),
x(x﹣1),
∴點E的坐標為(1,0).
設直線AE的解析式為y=k1x+b1,
將A(﹣1,1)、E(1,0)代入y=k1x+b1中,
![]() ,解得:
,解得: 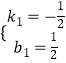 ,
,
∴直線AE的解析式為y=﹣ ![]() x+
x+ ![]() .
.
設直線FH的解析式為y=k2x+b2,
將F(0,m)、H(2m,0)代入y=k2x+b2中,
![]() ,解得:
,解得: 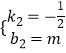 ,
,
∴直線FH的解析式為y=﹣ ![]() x+m.
x+m.
∴FH∥AE.
(3)設直線AB的解析式為y=k0x+b0,
將A(﹣1,1)、B(4,6)代入y=k0x+b0中,
![]() ,解得:
,解得: ![]() ,
,
∴直線AB的解析式為y=x+2.
當運動時間為t秒時,點P的坐標為(t﹣2,t),點Q的坐標為(t,0).
當點M在線段PQ上時,過點P作PP′⊥x軸于點P′,過點M作MM′⊥x軸于點M′,則△PQP′∽△MQM′,如圖2所示.
∵QM=2PM,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴QM′= ![]() ,MM′=
,MM′= ![]() t,
t,
∴點M的坐標為(t﹣ ![]() ,
, ![]() t).
t).
又∵點M在拋物線y= ![]() x2﹣
x2﹣ ![]() x上,
x上,
∴ ![]() t=
t= ![]() ×(t﹣
×(t﹣ ![]() )2﹣
)2﹣ ![]() (t﹣
(t﹣ ![]() ),
),
解得:t= ![]() ;
;
當點M在線段QP的延長線上時,
同理可得出點M的坐標為(t﹣4,2t),
∵點M在拋物線y= ![]() x2﹣
x2﹣ ![]() x上,
x上,
∴2t= ![]() ×(t﹣4)2﹣
×(t﹣4)2﹣ ![]() (t﹣4),
(t﹣4),
解得:t= ![]() .
.
綜上所述:當運動時間為 ![]() 秒、
秒、 ![]() 秒、
秒、 ![]() 秒或
秒或 ![]() 秒時,QM=2PM.
秒時,QM=2PM.
【解析】(1)利用待定系數法把A、B坐標代入解析式即可;(2)要證坐標系中的兩直線平行,可求兩直線的解析式,斜率k相等,兩直線平行,常數b可不必求出;(3)須動手畫出點M與線段PQ的兩種相對位置,分類討論,斜線段QM與PM的比,通過作垂線,轉化為x軸上水平線段的比,構建方程,求出t.
【考點精析】解答此題的關鍵在于理解二次函數的圖象的相關知識,掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,在菱形ABCD中,點E,O,F分別為AB,AC,AD的中點,連接CE,CF,OE,OF. 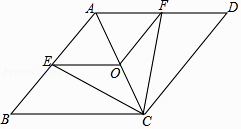
(1)求證:△BCE≌△DCF;
(2)當AB與BC滿足什么關系時,四邊形AEOF是正方形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,點
,點![]() 為
為![]() 內一點.
內一點.
(1)如圖1,連接![]() ,將
,將![]() 沿射線
沿射線![]() 方向平移,得到
方向平移,得到![]() ,點
,點![]() 的對應點分別為點
的對應點分別為點![]() ,連接
,連接![]() .如果
.如果![]() ,
,![]() ,則
,則![]() .
.
(2)如圖2,連接![]() ,當
,當![]() 時,求
時,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數y=![]() x+m (m為常數)的圖像與x軸交于點A(-3,0),與y軸交于點C.以直線x=1為對稱軸的拋物線y=ax2+bx+c(a,b,c為常數,且a≠0)經過A、C兩點,并與x軸的正半軸交于點B.
x+m (m為常數)的圖像與x軸交于點A(-3,0),與y軸交于點C.以直線x=1為對稱軸的拋物線y=ax2+bx+c(a,b,c為常數,且a≠0)經過A、C兩點,并與x軸的正半軸交于點B.
(1)求m的值及拋物線的函數表達式;
(2)若P是拋物線對稱軸上一動點,△ACP周長最小時,求出P的坐標;
(3)是否存在拋物在線一動點Q,使得△ACQ是以AC為直角邊的直角三角形?若存在,求出點Q的橫坐標;若不存在,請說明理由;
(4)在(2)的條件下過點P任意作一條與y軸不平行的直線交拋物線于M1(x1,y1),M2(x2,y2)兩點,試問![]() 是否為定值,如果是,請直接寫出結果,如果不是請說明理由.
是否為定值,如果是,請直接寫出結果,如果不是請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料I:
教材中我們學習了:若關于![]() 的一元二次方程
的一元二次方程![]() 的兩根為
的兩根為![]()
![]() ,根據這一性質,我們可以求出己知方程關于
,根據這一性質,我們可以求出己知方程關于![]() 的代數式的值.
的代數式的值.
問題解決:
(1)已知![]() 為方程
為方程![]() 的兩根,則:
的兩根,則:![]() __ _,
__ _,![]() __ _,那么_
__ _,那么_![]() (請你完成以上的填空)
(請你完成以上的填空)
閱讀材料:II
已知![]() ,且
,且![]() .求
.求![]() 的值.
的值.
解:由![]() 可知
可知![]()
![]()
![]()
又![]() 且
且![]() ,即
,即![]()
![]() 是方程
是方程![]() 的兩根.
的兩根.
![]()
問題解決:
(2)若![]() 且
且![]() 則
則![]() ;
;
(3)已知![]() 且
且![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y=![]() 的圖象經過點(﹣3,2).
的圖象經過點(﹣3,2).
(1)求它的解析式;
(2)在直角坐標中畫出該反比例函數的圖象;
(3)若﹣3<x<﹣2,求y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣ ![]() x2+
x2+ ![]() x+2與x軸交于點A,B,與y軸交于點C.
x+2與x軸交于點A,B,與y軸交于點C.
(1)試求A,B,C的坐標;
(2)將△ABC繞AB中點M旋轉180°,得到△BAD.
①求點D的坐標;
②判斷四邊形ADBC的形狀,并說明理由;
(3)在該拋物線對稱軸上是否存在點P,使△BMP與△BAD相似?若存在,請直接寫出所有滿足條件的P點的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】超速行駛是引發交通事故的主要原因.上周末,小鵬等三位同學在濱海大道紅樹林路段,嘗試用自己所學的知識檢測車速,觀測點設在到公路l的距離為100米的P處.這時,一輛富康轎車由西向東勻速駛來,測得此車從A處行駛到B處所用的時間為3秒,并測得∠APO=60°,∠BPO=45°,試判斷此車是否超過了每小時80千米的限制速度?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明就市電視臺的各節目所受歡迎的情況,對本班50名同學進行了一次調查,結果如下:
最受學生歡迎的電視節目
節目 | 人數 |
體育 | 18 |
新聞 | 16 |
綜藝 | 8 |
動畫 | 5 |
其他 | 3 |
(1)選用適當的統計圖描述上表數據;
(2)還能用其他統計圖描述嗎?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com