
【題目】把邊長分別為4和6的矩形ABCO如圖放在平面直角坐標系中,將它繞點C順時針旋轉a角,旋轉后的矩形記為矩形EDCF.在旋轉過程中,
(1)如圖①,當點E在射線CB上時,E點坐標為;
(2)當△CBD是等邊三角形時,旋轉角a的度數是(a為銳角時);
(3)如圖②,設EF與BC交于點G,當EG=CG時,求點G的坐標;
(4)如圖③,當旋轉角a=90°時,請判斷矩形EDCF的對稱中心H是否在以C為頂點,且經過點A的拋物線上.
【答案】
(1)(4,2 ![]() )
)
(2)60°
(3)
解.設CG=x,則EG=x,FG=6﹣x,
在Rt△FGC中,∵CF2+FG2=CG2,
∴42+(6﹣x)2=x2
解得 ![]() ,
,
即 ![]()
∴ ![]()
(4)
解.設以C為頂點的拋物線的解析式為y=a(x﹣4)2,
把A(0,6)代入,得6=a(0﹣4)2.
解得a= ![]() .
.
∴拋物線的解析式為y= ![]() (x﹣4)2
(x﹣4)2
∵矩形EDCF的對稱中心H即為對角線FD、CE的交點,
∴H(7,2).
當x=7時, ![]()
∴點H不在此拋物線上
【解析】解.(1)E(4,2 ![]() )
)
(1)依題意得點E在射線CB上,橫坐標為4,縱坐標根據勾股定理可得點E.(2)已知∠BCD=60°,∠BCF=30°,然后可得∠α=60°.(3)設CG=x,則EG=x,FG=6﹣x,根據勾股定理求出CG的值.(4)設以C為頂點的拋物線的解析式為y=a(x﹣4)2 , 把點A的坐標代入求出a值.當x=7時代入函數解析式可得解.


科目:初中數學 來源: 題型:
【題目】如圖,點B,F,C,E在直線l上(F,C之間不能直接測量),點A,D在l異側,測得AB=DE,AC=DF,BF=EC.

(1)求證:△ABC≌△DEF;
(2)指出圖中所有平行的線段,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點都在格點上, 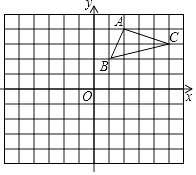
(1)①畫出△ABC關于x軸對稱的△A1B1C1 .
②畫出△ABC繞原點O旋轉180°后的△A2B2C2 , 并寫出A2、B2、C2的坐標
(2)假設每個正方形網格的邊長為1,求△A1B1C1的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的方程x2+ax+a﹣2=0
(1)若該方程的一個根為1,求a的值及該方程的另一根;
(2)求證:不論a取何實數,該方程都有兩個不相等的實數根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.試說明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題8分)如圖,在五邊形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求證:△ABC≌△AED;
(2)當∠B=140°時,求∠BAE的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,O為菱形ABCD對角線的交點,DE∥AC,CE∥BD. 
(1)試判斷四邊形OCED的形狀,并說明理由;
(2)若AC=6,BD=8,求線段OE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點B、E、C、F在一條直線上,AB=DF,AC=DE,∠A=∠D.
(1)求證:AC∥DE;
(2)若BF=13,EC=5,求BC的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com