
【題目】為迎接國慶節,某工廠生產一種火爆的紀念商品,每件商品成本25元,工廠將該商品進行網絡批發,批發單價![]() (元)與一次性批發量
(元)與一次性批發量![]() (件)(
(件)(![]() 為正整數)之間滿足如圖所示的函數關系.
為正整數)之間滿足如圖所示的函數關系.

(1)求![]() 與
與![]() 的函數解析式(也稱關系式).
的函數解析式(也稱關系式).
(2)若一次性批發量超過20且不超過50件時,求獲得的利潤![]() 與
與![]() 的函數關系式,同時求當批發量為多少件時,工廠獲利最大?最大利潤是多少?
的函數關系式,同時求當批發量為多少件時,工廠獲利最大?最大利潤是多少?
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O是△ABC的外接圓,AC是直徑,∠A=30°,BC=2,點D是AB的中點,連接DO并延長交⊙O于點P,過點P作PF⊥AC于點F.
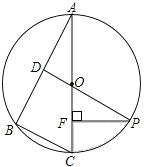
(1)求劣弧PC的長;(結果保留π)
(2)求陰影部分的面積.(結果保留π).
查看答案和解析>>
科目:初中數學 來源: 題型:
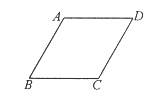
【題目】如圖,在菱形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是這個菱形內部或邊上的一點,若以點
是這個菱形內部或邊上的一點,若以點![]() ,
,![]() ,
,![]() 為頂點的三角形是等腰三角形,則
為頂點的三角形是等腰三角形,則![]() ,
,![]() (
(![]() ,
,![]() 兩點不重合)兩點間的最短距離為( )
兩點不重合)兩點間的最短距離為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,E為BC邊上一動點(不與點B、C重合),延長AE到點F,連接BF,且∠AFB=45°,G為DC邊上一點,且DG=BE,連接DF,點F關于直線AB的對稱點為M,連接AM、BM.
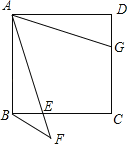
(1)依據題意,補全圖形;
(2)求證:∠DAG=∠MAB;
(3)用等式表示線段BM、DF與AD的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐
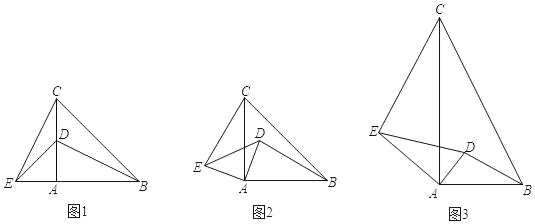
問題情境:如圖1,在數學活動課上,老師讓同學們畫了等腰Rt△ABC和等腰Rt△ADE,并連接CE,BD.
操作發現:(1)當等腰Rt△ADE繞點A旋轉,如圖2,勤奮小組發現了:
①線段CE與線段BD之間的數量關系是 .
②直線CE與直線BD之間的位置關系是 .
類比思考:(2)智慧小組在此基礎上進行了深入思考,如圖3,若△ABC與△ADE都為直角三角形,∠BAC=∠DAE=90°,且AC=2AB,AE=2AD,請你寫出CE與BD的數量關系和位置關系,并加以證明.
拓展應用:(3)創新小組在(2)的基礎上,又作了進一步拓展研究,當點E在直線AB上方時,若DE∥AB,且AB=![]() ,AD=1,其他條件不變,試求出線段CE的長.(直接寫出結論)
,AD=1,其他條件不變,試求出線段CE的長.(直接寫出結論)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以A(0, ![]() )為圓心的圓與x軸相切于坐標原點O,與y軸相交于點B,弦BD的延長線交x軸的負半軸于點E,且∠BEO=60°,AD的延長線交x軸于點C.
)為圓心的圓與x軸相切于坐標原點O,與y軸相交于點B,弦BD的延長線交x軸的負半軸于點E,且∠BEO=60°,AD的延長線交x軸于點C.
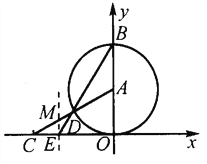
(1)分別求點E、C的坐標;
(2)求經過A、C兩點,且以過E而平行于y軸的直線為對稱軸的拋物線的函數解析式;
(3)設拋物線的對稱軸與AC的交點為M,試判斷以M點為圓心,ME為半徑的圓與⊙A的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,基燈塔AB建在陡峭的山坡上,該山坡的坡度i=1:0.75.小明為了測得燈塔的高度,他首先測得BC=20m,然后在C處水平向前走了34m到達一建筑物底部E處,他在該建筑物頂端F處測得燈塔頂端A的仰角為43°.若該建筑物EF=20m,則燈塔AB的高度約為(精確到0.1m,參考數據:sin43°=0.68,cos43°=0.73,tan43°=0.93)( )
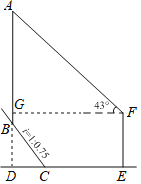
A.46.7mB.46.8mC.53.5mD.67.8m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學全體同學參加了“關懷貧困學生”愛心捐款活動,該校隨機抽查了七、八、九三個年級部分學生捐款情況,將結果繪制成兩幅不完整的統計圖.根據圖中的信息,解決下列問題:
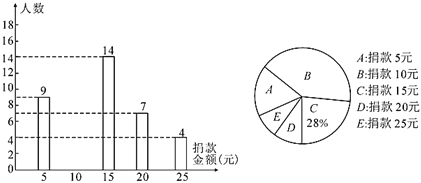
(1)這次共抽查了_______名學生進行統計,其中![]() 類所對應扇形的圓心角的度數為________;
類所對應扇形的圓心角的度數為________;
(2)將條形統計圖補充完整;
(3)該校有![]() 名學生,估計該校捐款
名學生,估計該校捐款![]() 元的學生有多少人?
元的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
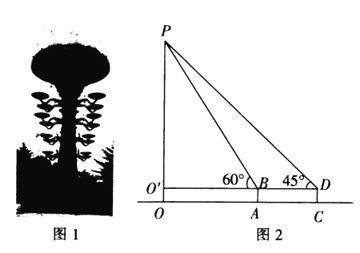
【題目】如圖1所示的是寶雞市文化景觀標志“天下第一燈”,它由國際![]() 不銹鋼板整體鍛造,表面涂有仿古金色漆,以仿青銅紋飾雕刻的柱體四盞燈分
不銹鋼板整體鍛造,表面涂有仿古金色漆,以仿青銅紋飾雕刻的柱體四盞燈分![]() 層布置.一天上午,數學興趣小組的同學們帶著測量工具來測量“天下第一燈”的高度,由于有圍欄保護,他們無法到達燈的底部
層布置.一天上午,數學興趣小組的同學們帶著測量工具來測量“天下第一燈”的高度,由于有圍欄保護,他們無法到達燈的底部![]() 他們制定了一種測量方案,圖2所示的是他們測量方案的示意圖,先在周圍的廣場上選擇一點
他們制定了一種測量方案,圖2所示的是他們測量方案的示意圖,先在周圍的廣場上選擇一點![]() 并在點
并在點![]() 處安裝了測量器
處安裝了測量器![]() 在點
在點![]() 處測得該燈的頂點P的仰角為
處測得該燈的頂點P的仰角為![]() ;再在
;再在![]() 的延長線上確定一點
的延長線上確定一點![]() 使
使![]() 米,在
米,在![]() 點處測得該燈的頂點
點處測得該燈的頂點![]() 的仰角為
的仰角為![]() .若測量過程中測量器的高度始終為
.若測量過程中測量器的高度始終為![]() 米,求“天下第一燈”的高度.
米,求“天下第一燈”的高度.![]() ,最后結果取整數)
,最后結果取整數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com