
【題目】如圖,AB∥CD,AD與BC相交于點E,AF平分∠BAD,交BC于點F,交CD的延長線于點G.

(1)若∠G=29°,求∠ADC的度數;
(2)若點F是BC的中點,求證:AB=AD+CD.
【答案】(1)58°;(2)詳見解析
【解析】
(1)根據平行和角平分線,可推導出∠ADC=2∠G,從而得出∠ADC的大小;
(2)證△ABF≌△GCF,從而得出AB=GC,從而證AB=AD+CD.
證明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵點F是BC的中點,∴BF=CF.
在△ABF和△GCF中,
∵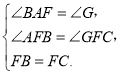
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:初中數學 來源: 題型:
【題目】新型冠狀病毒肺炎疫情發生后,全社會的積極參與疫情防控工作下,才有了我們的平安復學.為了能在復學前將一批防疫物資送達校園,某運輸公司組織了甲、乙兩種貨車,已知甲種貨車比乙種貨車每輛車多裝20箱防疫物資,且甲種貨車裝運900箱防疫物資所用車輛與乙種貨車裝運600箱防疫物資所用的車輛相等,求甲、乙兩種貨車每輛車可裝多少箱防疫物資?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() ,
,![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .直線
.直線![]() 經過點
經過點![]() ,
,![]() .
.
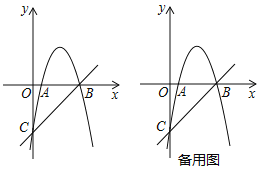
(1)求拋物線的解析式;
(2)過點![]() 的直線交直線
的直線交直線![]() 于點
于點![]() .
.
①當![]() 時,過拋物線上一動點
時,過拋物線上一動點![]() (不與點
(不與點![]() ,
,![]() 重合),作直線
重合),作直線![]() 的平行線交直線
的平行線交直線![]() 于點
于點![]() ,若以點
,若以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是平行四邊形,求點
為頂點的四邊形是平行四邊形,求點![]() 的橫坐標;
的橫坐標;
②連接![]() ,當直線
,當直線![]() 與直線
與直線![]() 的夾角等于
的夾角等于![]() 的
的![]() 倍時,請直接寫出點
倍時,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,點
兩點,點![]() 的坐標為
的坐標為![]() .
.
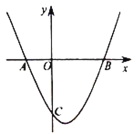
(1)求![]() 點坐標;
點坐標;
(2)若對于每一個給定的![]() 的值,它所對應的函數值都不小于
的值,它所對應的函數值都不小于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(3)直線![]() 經過點
經過點![]() .
.
①求直線和拋物線的解析式;
②設拋物線與![]() 軸的交點為
軸的交點為![]() ,過點
,過點![]() 作直線
作直線![]() 軸,將拋物線在
軸,將拋物線在![]() 軸左側的部分沿直線
軸左側的部分沿直線![]() 翻折,拋物線的其余部分保持不變,得到一個新圖像,請你結合新圖像回答:
翻折,拋物線的其余部分保持不變,得到一個新圖像,請你結合新圖像回答:
當直線![]() 與新圖像只有一個公共點
與新圖像只有一個公共點![]() 且
且![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在正方形ABCD中,點E是邊BC上一點,連接AE,過點E作EM⊥AE,交對角線AC于點M,過點M作MN⊥AB,垂足為N,連接NE.
(1)求證:AE=![]() NE+ME;
NE+ME;
(2)如圖2,延長EM至點F,使EF=EA,連接AF,過點F作FH⊥DC,垂足為H.
猜想CH與FH存在的數量關系,并證明你的結論;
(3)在(2)的條件下,若點G是AF的中點,連接GH.當GH=CH時,直接寫出GH與AC之間存在的數量關系.
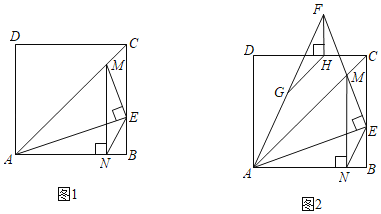
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,一次函數y1=ax+b(a,b為常數,且a≠0)與反比例函數y2=![]() (m為常數,且n≠0)的圖象交于點A(﹣3,1)、B(1,n).
(m為常數,且n≠0)的圖象交于點A(﹣3,1)、B(1,n).
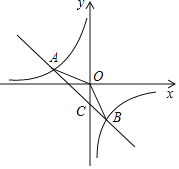
(1)求反比例函數和一次函數的解析式;
(2)連結0A、OB,求△AOB的面積;
(3)直接寫出當y1<y2<0時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織學生開展義務植樹活動,在活動結束后隨機調查了40名學生每人植樹的棵數,根據調查獲取的樣本數據,制作了條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:
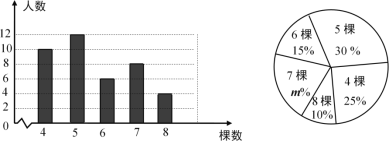
(1)扇形圖中![]() 的值是_________;
的值是_________;
(2)求隨機調查的40名學生每人植樹棵數這組數據的平均數、眾數和中位數;
(3)若本次活動九年級共有300名學生參加,估計植樹超過6棵(不含6棵)的學生約有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某開發商原計劃對樓盤新房以每平方米4000元的銷售價對外銷售.現為了加快資金周轉,對銷售價經過兩次下調后,決定在開盤之日以每平方米3240元的銷售價進行促銷.
(1)求銷售價平均每次下調的百分率;
(2)開盤之日,開發商又給予以下兩種優惠方案以供選擇:方案①一次性送裝修費每平方米50元;方案②打9.8折銷售.張先生要購買一套100平方米的住房,試問哪種方案更優惠?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com