【題目】如圖，在△ABC中，∠C＝90°，∠B＝30°，以A為圓心，任意長為半徑畫弧分別交AB、AC于點M和N，再分別以M、N為圓心，大于
MN的長為半徑畫弧，兩弧交于點P，連接AP，并延長交BC于點D，則下列說法中正確的個數是（ ）
①AD是∠BAC的平分線；②∠ADC＝60°；③點D在AB的垂直平分線上；④若AC=
dm，AD=2dm，則點D到AB的距離是1dm；⑤S△DAC∶S△DAB＝AC∶AB＝1∶2
A. 2 B. 3 C. 4 D. 5
【答案】D
【解析】①根據作圖的過程可知，AD是∠BAC的平分線；故①正確；
②如圖，
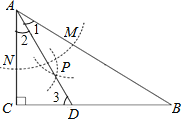
∵在△ABC中，∠C=90，∠B=30°，∴∠CAB=60°.
又∵AD是∠BAC的平分線，∴∠1=∠2=
∠CAB=30°，
∴∠3=90°∠2=60°，即∠ADC=60°.故②正確；
③∵∠1=∠B=30°，∴AD=BD，∴點D在AB的垂直平分線上；故③正確；
④∵∠C＝90°，AC=
dm，AD=2dm，∴CD=1cm，
如圖，過D作DE⊥AB于點E，
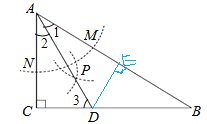
∵AD是∠CAB的平分線，DC⊥AC，DE⊥AB，
∴CD=ED， ∴ED=1cm，故④正確；
（5）在直角△ACD中，∠2=30°，
∴CD=
AD，
∴BC=CD+BD=
AD+AD=
AD，S△DAC=
ACCD=
ACAD.
∴S△ABD=
ACBD=
ACAD=
ACAD，
∴S△DAC:S△ABD=
ACAD: 
ACAD=1:2.故⑤正確.
綜上所述，正確的結論是：①②③④⑤.
故選：D.
科目：初中數學 來源： 題型：
【題目】已知△ABC的三個頂點分別是A（4，3），B（2，-1），C（-2，1）．現平移△ABC使它的一個頂點與坐標原點重合，則平移后點A的坐標是 .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校組織學生書法比賽，對參賽作品按A、B、C、D四個等級進行了評定．現隨機抽取部分學生書法作品的評定結果進行分析，并繪制扇形統計圖和條形統計圖如下：
根據上述信息完成下列問題：
（1）求本次調查共抽取了多少份書法作品？
（2）請在圖②中把條形統計圖補充完整；
（3）已知該校這次活動共收到參賽作品750份，請你估計參賽作品達到B級以上（即A級和B級）有多少份？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，點O為坐標原點，拋物線y=-
x2+bx+c交x軸于A、B兩點，交y軸于點C,直線y=x+6經過A、C兩點．
（1）求拋物線的解析式；
（2）點P是第二象限拋物線上的一個動點，過點P作PQ∥AC,PQ交直線BC于點Q，設點P的橫坐標為t，點Q的橫坐標為m,求m與t之間的函數關系式（不要求寫出自變量t的取值范圍）；
（3）在（2）的條件下，作點P關于直線AC的對稱點點K,連接QK,當點K落在直線y=-
x上時，求線段QK的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校八年級數學興趣小組的同學調查了若干名家長對“初中生帶手機上學”現象的看法，統計整理并制作了如下的條形與扇形統計圖。依據圖中信息，解答下列問題：
（1）接受這次調查的家長共有 人；
（2）補全條形統計圖；
（3）在扇形統計圖中，“很贊同”的家長占被調查家長總數的百分比是 ；
（4）在扇形統計圖中，“不贊同”的家長部分所對應扇形的圓心角度數是 度．
（5）請同學們對“初中生帶手機上學”現象說說你的看法.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC是以BC為底的等腰三角形，AD是邊BC上的高，點E、F分別是AB、AC的中點．
（1）求證：四邊形AEDF是菱形；
（2）如果四邊形AEDF的周長為12，兩條對角線的和等于7，求四邊形AEDF的面積S．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB=AC，∠ABC=72°．
（1）用直尺和圓規作∠ABC的平分線BD交AC于點D（保留作圖痕跡，不要求寫作法）；
（2）在（1）中作出∠ABC的平分線BD后，求∠BDC的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，點P是∠ABC內一點．
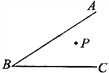
(1)畫圖：①過點P畫BC的垂線，垂足為D；②過點P畫BC的平行線交AB于點E，過點P畫AB的平行線交BC于點F．
(2)∠EPF等于∠B嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
