
【題目】如圖,△ABC是以BC為底的等腰三角形,AD是邊BC上的高,點E、F分別是AB、AC的中點.
(1)求證:四邊形AEDF是菱形;
(2)如果四邊形AEDF的周長為12,兩條對角線的和等于7,求四邊形AEDF的面積S.

【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)利用直角三角形斜邊中線是斜邊一半,求得DE=AE=AF=DF,
所以AEDF是菱形.
(2)由(1)得,AEDF是菱形,求得菱形對角線乘積的一半,求面積 .
試題解析:
(1)∵AD⊥BC,點E、F分別是AB、AC的中點,
∴Rt△ABD中,DE=![]() AB=AE,
AB=AE,
Rt△ACD中,DF=![]() AC=AF,
AC=AF,
又∵AB=AC,點E、F分別是AB、AC的中點,
∴AE=AF,
∴AE=AF=DE=DF,
∴四邊形AEDF是菱形.
(2)如圖,∵菱形AEDF的周長為12,
∴AE=3,
設EF=x,AD=y,則x+y=7,
∴x2+2xy+y2=49,①
∵AD⊥EF于O,
∴Rt△AOE中,AO2+EO2=AE2,
∴(![]() y)2+(
y)2+(![]() x)2=32,
x)2=32,
即x2+y2=36,②
把②代入①,可得2xy=13,
∴xy=![]() ,
,
∴菱形AEDF的面積S=![]() xy=
xy=![]() .
.



科目:初中數學 來源: 題型:
【題目】.如圖,點A、B、D、E在⊙O上,弦AE、BD的延長線相交于點C.若AB是⊙O的直徑,D是BC的中點.
(1)試判斷AB、AC之間的大小關系,并給出證明;
(2)在上述題設條件下,當△ABC為正三角形時,點E是否AC的中點?為什么?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .說明
.說明![]() 的理由.
的理由.

解:因為![]() (已知),
(已知),
所以![]() ∥
∥![]() (________________________________).
(________________________________).
所以![]() (_____________________________).
(_____________________________).
因為![]() 平分
平分![]() (已知),
(已知),
所以![]() (_______________________________).
(_______________________________).
同理![]() .
.
所以![]() (___________________________________).
(___________________________________).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連接AP,并延長交BC于點D,則下列說法中正確的個數是( )
MN的長為半徑畫弧,兩弧交于點P,連接AP,并延長交BC于點D,則下列說法中正確的個數是( )

①AD是∠BAC的平分線;②∠ADC=60°;③點D在AB的垂直平分線上;④若AC=![]() dm,AD=2dm,則點D到AB的距離是1dm;⑤S△DAC∶S△DAB=AC∶AB=1∶2
dm,AD=2dm,則點D到AB的距離是1dm;⑤S△DAC∶S△DAB=AC∶AB=1∶2
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】己知:如圖①,直線![]() 直線
直線![]() ,垂足為
,垂足為![]() ,點
,點![]() 在射線
在射線![]() 上,點
上,點![]() 在射線
在射線![]() 上(
上(![]() 、
、![]() 不與
不與![]() 點重合),點
點重合),點![]() 在射線
在射線![]() 上且
上且![]() ,過點
,過點![]() 作直線
作直線![]() .點
.點![]() 在點
在點![]() 的左邊且
的左邊且![]()

(1)直接寫出的![]() 面積 ;
面積 ;
(2)如圖②,若![]() ,作
,作![]() 的平分線交
的平分線交![]() 于
于![]() ,交
,交![]() 于
于![]() ,試說明
,試說明![]() ;
;


(3)如圖③,若![]() ,點
,點![]() 在射線
在射線![]() 上運動,
上運動,![]() 的平分線交
的平分線交![]() 的延長線于點
的延長線于點![]() ,在點
,在點![]() 運動過程中
運動過程中![]() 的值是否變化?若不變,求出其值;若變化,求出變化范圍.
的值是否變化?若不變,求出其值;若變化,求出變化范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O的圓心在定角∠α(0°<α<180°)的角平分線上運動,且⊙O與∠α的兩邊相切,圖中陰影部分的面積S關于⊙O的半徑r(r>0)變化的函數圖象大致是( )
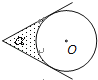
A. 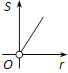 B.
B. 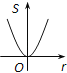 C.
C. 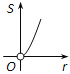 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠MON=80°,OE平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O 重合),連接AC交射線OE于點D.設∠OAC=x°.
(1)如圖1,若AB∥ON,則:①∠ABO的度數是 ;
②如圖2,當∠BAD=∠ABD時,試求x的值(要說明理由);
(2)如圖3,若AB⊥OM,則是否存在這樣的X的值,使得△ADB中有兩個相等的角?若存在,直接寫出x的值;若不存在,說明理由.(自己畫圖)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com