
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展,小明計劃給朋友快遞一部分物品,經了解有甲乙兩家快遞公司比較合適.甲公司表示:快遞物品不超過1千克的,按每千克22元收費;超過1千克,超過的部分按每千克15元收費,乙公司表示:按每千克16元收費,另加包裝費3元,設小明快遞物品x千克.
(1)根據題意,填寫下表:
快遞物品重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司收費(元) | 22 | … | |||
乙公司收費(元) | 11 | 51 | 67 | … |
(2)設甲快遞公司收費y1元,乙快遞公司收費y2元,分別寫出y1,y2關于x的函數關系式;
(3)當x>3時,小明應選擇哪家快遞公司更省錢?請說明理由.
【答案】(1)11,19,52,67;(2)![]() ;y2=16x+3;(3)當3<x<4時,小明應選擇乙公司省錢;當x=4時,兩家公司費用一樣;當x>4,小明應選擇甲公司省錢.
;y2=16x+3;(3)當3<x<4時,小明應選擇乙公司省錢;當x=4時,兩家公司費用一樣;當x>4,小明應選擇甲公司省錢.
【解析】
(1)根據甲、乙公司的收費方式,求出y值即可;
(2)根據甲、乙公司的收費方式結合數量關系,找出y1、y2(元)與x(千克)之間的函數關系式;
(3)x>3,分別求出y1>y2、y1=y2、y1<y2時x的取值范圍,綜上即可得出結論.
解:(1)當x=0.5時,y甲=22×0.5=11;
當x=1時,y乙=16×1+3=19;
當x=3時,y甲=22+15×2=52;
當x=4時,y甲=22+15×3=67.
故答案為:11;19;52;67.
(2)當0<x≤1時,y1=22x;
當x>1時,y1=22+15(x-1)=15x+7.
∴ ![]()
y2=16x+3(x>0);
(3)當x>3時,
當y1>y2時,有15x+7>16x+3,
解得:x<4;
當y2=y2時,有15x+7=16x+3,
解得:x=4;
當y1<y2時,有15x+7<16x+3,
解得:x>4.
∴當3<x<4時,小明應選擇乙公司省錢;當x=4時,兩家公司費用一樣;當x>4,小明應選擇甲公司省錢.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖1所示的是帶支架功能的某品牌手機殼,將其側面抽象為如圖2所示的幾何圖形,已知AB=5cm,∠BAC=60°,∠C=45°,則AC的長(![]() ≈1.732,結果精確到0.1cm)為( )
≈1.732,結果精確到0.1cm)為( )
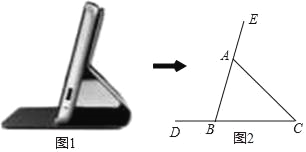
A. 3.4cm B. 4.6cm C. 5.8cm D. 6.8cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABO中,斜邊AB=1,若OC∥BA,∠AOC=36°,則( )
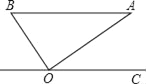
A. 點B到AO的距離為sin54°
B. 點A到OC的距離為sin36°sin54°
C. 點B到AO的距離為tan36°
D. 點A到OC的距離為cos36°sin54°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD的邊長為4,點E、F分別在邊AB、BC上,且AE=BF=1,CE、DF相交于點O,下列結論:
①∠DOC=90°,②OC=OE,③tan∠OCD=![]() ,④△COD的面積等于四邊形BEOF的面積,正確的有 ( )
,④△COD的面積等于四邊形BEOF的面積,正確的有 ( )
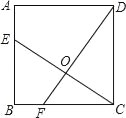
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上兩點A,B表示的數分別為﹣2,6,用符號“AB”來表示點A和點B之間的距離.
![]()
(1)求AB的值;
(2)若在數軸上存在一點C,使AC=3BC,求點C表示的數;
(3)在(2)的條件下,點C位于A、B兩點之間.點A以1個單位/秒的速度沿著數軸的正方向運動,2秒后點C以2個單位/秒的速度也沿著數軸的正方向運動,到達B點處立刻返回沿著數軸的負方向運動,直到點A到達點B,兩個點同時停止運動.設點A運動的時間為t,在此過程中存在t使得AC=3BC仍成立,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算與簡化:
(1)﹣22﹣[(1﹣1×0.6)+(﹣0.2)2﹣4]
(2)![]() (2a2﹣9b)﹣3(﹣5a2﹣
(2a2﹣9b)﹣3(﹣5a2﹣![]() b)﹣3b
b)﹣3b
(3)x﹣![]() =
=![]() +2
+2
(4)![]() =
=![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有理數數a,b在軸上的表示如圖所示,則下列結論中:①ab<0,②a+b<0,③a﹣b<0,④a<![]() ,⑤﹣a>﹣b,正確的有( )
,⑤﹣a>﹣b,正確的有( )
![]()
A.2個B.3個C.4個D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
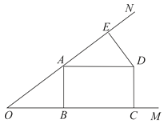
【題目】如圖,點A在∠MON的邊ON上,AB⊥OM于B,AE=OB,DE⊥ON于E,AD=AO,DC⊥OM于C.
(1)求證:四邊形ABCD是矩形;
(2)若DE=3,OE=9,求AB、AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 A 處觀察 C 測得仰角∠CAD=31°,且 A、B 的水平距離 AE=800 米,斜坡 AB 的坡度i 1: 2 ,索道 BC 的坡度i 2 : 3 ,CD⊥AD 于 D,BF⊥CD 于 F,則索道BC 的長大約是( )
(參考數據:tan31°≈0. cos31°≈0.9,![]() ≈3.6)
≈3.6)

A. 1400 B. 1440 C. 1500 D. 1540
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com