
【題目】如圖,在△ABC中,AB=2,BC=4,其兩條外角平分線AD、CD交于點D,且∠ADC=45°,連接BD交AC于點P,過點P作PE⊥AC交BC于點F,交AB的延長線于點E.
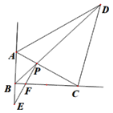
(1)求證:∠ABC=90° ;
(2)求S△PFC:S△PBF的值.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)設∠BAC=![]() ,∠ACB=
,∠ACB=![]() ,然后分別表示出∠DAC和∠DCA,利用三角形內角和可求出
,然后分別表示出∠DAC和∠DCA,利用三角形內角和可求出![]() ,即可得證;
,即可得證;
(2)由角平分線的性質易得BD平分∠ABC,過P作PG⊥BD,易證△PBE≌△PGC,然后證明△PCF≌△PEA,可得CF=AE,設BF=x,則CF=AE=4-x,可得BE=2-x,由BF與BE的比例關系可解出x,得到BF與FC的比例關系即為面積比.
解:(1)設∠BAC=![]() ,∠ACB=
,∠ACB=![]() ,
,
∵AD、CD為△ABC的外角平分線,
∴∠DAC=![]()
∠DCA=![]()
在△ACD中,∠DAC+∠ACD+∠ADC=180°,
即![]()
∴![]()
∴∠ABC=![]()
(2)如圖所示,過D作DN⊥AB于點N,DM⊥BC于點M,DH⊥AC于點H,
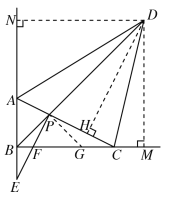
∵AD平分∠CAN,CD平分∠ACM,
∴DN=DH,DH=DM
∴DN=DM
∴BD平分∠ABC
又∵∠ABC=90°,
∴∠PBC=45°,
過P作PG⊥PB,交BC于點G,如圖,
∴∠PBG=∠PGB=45°
∴PB=PG
∵∠PCG+∠BAC=90°,∠E+∠BAC=90°
∴∠PCG=∠E
∵PE⊥AC
∴∠CPG+∠GPF=90°
又∵∠EPB+∠GPF=90°
∴∠CPG=∠EPB
在△PBE和△PGC中,
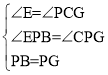
∴△PBE≌△PGC(AAS)
∴PE=PC
在△PCF和△PEA中,
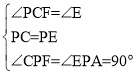
∴△PCF≌△PEA(ASA)
∴CF=AE
設BF=x,則CF=AE=4-x,BE=AE-AB=2-x,
∵∠ACB=∠E,∠ABC=∠FBE=90°,
∴△ABC∽△FBE
∴![]()
即![]() ,解得x=
,解得x=![]()
∴CF=![]()
∴![]()
即S△PFC:S△PBF的值為![]() .
.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,某同學把一塊三角形的玻璃打碎成了三塊,現在要到玻璃店去配一塊完全一樣的玻璃,那么最省事的辦法是( )

A.帶①去B.帶②去C.帶③去D.帶①和②去
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校七年級準備購買一批筆記本獎勵優秀學生,在購買時發現,每本筆記本可以打九折,用360元錢購買的筆記本,打折后購買的數量比打折前多10本.
(1)求打折前每本筆記本的售價是多少元?
(2)由于考慮學生的需求不同,學校決定購買筆記本和筆袋共90件,筆袋每個原售價為6元,兩種物品都打九折,若購買總金額不低于360元,且不超過365元,問有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,已知△ABC為等邊三角形,動點D在邊AC上,動點P在邊BC上,若這兩點分別從C、B點同時出發,以相同的速度由C向A和由B向C運動,連結AP、BD交于Q,兩點運動的過程中,AP=BD成立嗎?請證明你的結論.
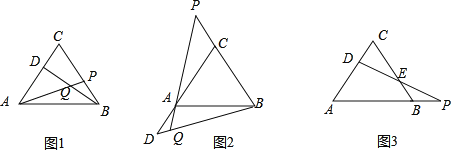
(2)如果把原題中的“動點D在邊AC上,動點P在邊BC上,”改為:“動點D在射線CA上、動點P在射線BC上運動,”其他條件不變,如圖2所示,AP=BD還成立嗎?說明理由,并求出∠BQP的大小.
(3)如果把原題中的“動點P在邊BC上”,改為“動點P在射線AB上運動”,連結DP交BC于E,其他條件不變,如圖3,則動點D、P在運動過程中,請你寫出DE與PE的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某校綜合實踐活動小組的同學欲測量公園內一棵樹DE的高度.他們在這棵樹正前方一座樓亭前的臺階上A點處測得樹頂端D的仰角為30°,朝著這棵樹的方向走到臺階下的點C處,測得樹頂端D的仰角為60°.已知A點的高度AB為2米,臺階AC的坡度為1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度(測傾器的高度忽略不計).
),且B、C、E三點在同一條直線上.請根據以上條件求出樹DE的高度(測傾器的高度忽略不計).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:BF為△ABC的外角∠ABE的平分線,D為BF上一點,且AD=CD.
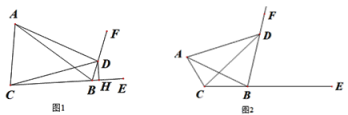
(1)如圖1,過點D作DH⊥CE于點H,若AB=8,BC=6,求BH的長.
(2)如圖2,若∠ABC=24°,∠ABD=78°,∠BAD=60°,求∠BAC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
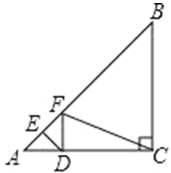
【題目】動手操作:如圖,在Rt△ABC中,∠ACB=90°,AC=8,BC=4,點D為邊AC上一動點,DE⊥AB交AB于點E,將∠A沿直線DE折疊,點A的對應點為F.當△DFC是直角三角形時,AD的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,AB=AC,D、E是斜邊BC上兩點,且∠DAE=45°,將△ADC繞點A順時針旋轉90°后,得到△AFB,連接EF,下列結論①△AEF≌△AED;②∠AED=45°;③BE+DC=DE; ④BE![]() +DC
+DC![]() =DE
=DE![]() ,其中正確的是( )
,其中正確的是( )

A. ②④ B. ①④ C. ②③ D. ①③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com