
【題目】若關于 x 的一元二次方程axbxc=0(a0,c0,a、b、c為常數)有兩個不相等的實數根![]() ,
,![]() (0
(0![]()
![]() ),O為坐標原點,A、B為x軸正半軸上的兩點且A
),O為坐標原點,A、B為x軸正半軸上的兩點且A![]() ,0,B
,0,B![]() ,0.
,0.
(1)當![]() =c=2,b=-
=c=2,b=-![]() 時,求
時,求![]() 與a的值;
與a的值;
(2)當 x 1,c 6a 時,P為一次函數 y x4圖象上一點,Q為平面直角坐標系中的一點,若點 A、B、P、Q 為一個矩形的四個頂點,請確定點Q的坐標;
(3)當![]() =2c時,試問在正比例函數y=
=2c時,試問在正比例函數y=![]() 的圖象上是否存在點M使得△ABM為等邊三角形?判斷并證明你的結論。
的圖象上是否存在點M使得△ABM為等邊三角形?判斷并證明你的結論。

【答案】(1)![]() =3,a=
=3,a=![]() ;(2)點Q的坐標為:(6,3)或(1,-2);(3)不存在點M使得△ABM為等邊三角形,證明見解析.
;(2)點Q的坐標為:(6,3)或(1,-2);(3)不存在點M使得△ABM為等邊三角形,證明見解析.
【解析】
(1)把![]() =c=2,b=
=c=2,b=![]() 代入可求出a的值,從而得到該方程,利用根與系數的關系可求出另一根;
代入可求出a的值,從而得到該方程,利用根與系數的關系可求出另一根;
(2)把x1,c6a代入可求出b=-7a,從而將方程變形為a(x-1)(x-6)=0,得到A,B坐標,然后根據一次函數圖像上點的坐標特征和矩形的性質可分情況求出點Q的坐標;
(3)將![]() =2c代入axbx c=0利用根與系數的關系求出
=2c代入axbx c=0利用根與系數的關系求出![]() ,得到A,B坐標,過點M作MC⊥x軸于點C,由C是AB中點,可求出C的坐標,進而代入正比例函數解析式得到M點坐標,然后根據CM=
,得到A,B坐標,過點M作MC⊥x軸于點C,由C是AB中點,可求出C的坐標,進而代入正比例函數解析式得到M點坐標,然后根據CM=![]() AC列出方程求出b值,推出矛盾,問題得解.
AC列出方程求出b值,推出矛盾,問題得解.
解:(1)把![]() =c=2,b=
=c=2,b=![]() 代入ax bx c=0得:4a+2×(
代入ax bx c=0得:4a+2×(![]() )+2=0,
)+2=0,
解得:a=![]() ,
,
所以該方程為:![]() x
x![]() x 2=0,
x 2=0,
∵![]() =
=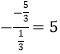 ,即2+
,即2+![]() =5,
=5,
∴![]() =3;
=3;
(2)把x1,c6a代入axbx c=0得ab6a=0,
∴b=-7a;
∴ax-7ax 6a=0,即a(xx 6)=0,
∴a(x-1)(x-6)=0(a0),
∴![]() ,
,![]() ,
,
∴A(1,0),B(6,0),
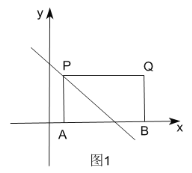
①如圖1,過點A作AP⊥x軸交直線yx4于點P,
∴P(1,3),
∵四邊形APQB為矩形,
∴Q(6,3);
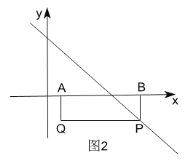
②如圖2,過點B作BP⊥x軸交直線yx4于點P,
∴P(6,-2),
∵四邊形ABPQ為矩形,
∴Q(1,-2);
綜上所述,點Q的坐標為:(6,3)或(1,-2);
(3)不存在點M使得△ABM為等邊三角形;
證明:將![]() =2c代入axbx c=0得:4ac2+2bc+c=0,即c(4ac+2b+1)=0,
=2c代入axbx c=0得:4ac2+2bc+c=0,即c(4ac+2b+1)=0,
∵c0,
∴4ac+2b+1=0①,
∵![]() ,
,
∴![]() ,
,
∴A(2c,0),B(![]() ,0),
,0),
假設存在點M使得△ABM為等邊三角形,
如圖3,過點M作MC⊥x軸于點C,則C是AB中點,
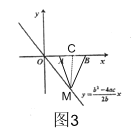
∴C點橫坐標為:![]() ,
,
將![]() 代入
代入![]() 可得
可得![]() ,
,
由①可知4ac=-(2b+1),4ac+1=-2b,
∴![]() ,
,
∴M(![]() ,
,![]() ),
),
當△ABM為等邊三角形時,CM=![]() AC,
AC,
AC![]() ,
,
∴![]()
∴![]() ,
,
解得:b=-1(舍)或b=![]() ,
,
∵b=![]() ,
,![]() ,
,
∴a<0,與題設中a0矛盾,
∴不存在點M使得△ABM為等邊三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】為了進一步改善環境,鄭州市今年增加了綠色自行車的數量,已知A型號的自行車比B型號的自行車的單價低30元,買8輛A型號的自行車與買7輛B型號的自行車所花費用相同.
(1)A,B兩種型號的自行車的單價分別是多少?
(2)若購買A,B兩種自行車共600輛,且A型號自行車的數量不多于B型號自行車的一半,請你給出一種最省錢的方案,并求出該方案所需要的費用.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A(1,a)是反比例函數![]() 的圖象上一點,直線
的圖象上一點,直線![]() 與反比例函數
與反比例函數![]() 的圖象在第四象限的交點為點B.
的圖象在第四象限的交點為點B.
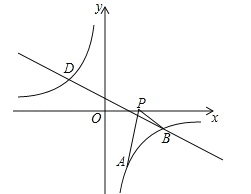
(1)求直線AB的解析式;
(2)動點P(x,0)在x軸的正半軸上運動,當線段PA與線段PB之差達到最大時,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
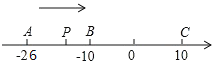
【題目】已知數軸上有A、B、C三點,分別表示有理數﹣26,﹣10,10,動點P從A出發,以每秒1個單位的速度向右移動,當P點運動到C點時運動停止,設點P移動時間為t秒。
(1)用含t的代數式表示P到點A和點C的距離:PA=_____,PC=_____.
(2)當點P運動到B點時,點Q從A出發,以每秒3個單位的速度向右運動,求t等于多少秒時P、Q兩點相遇?t等于多少秒時P、Q兩點相距4個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A,B兩點在同一條數軸上,點A在原點的左邊,到原點的距離為4,點B在原點右邊,點A 到B點的距離為16.
(1)求A,B兩點所表示的數:
(2)若A,B兩點分別以每秒1個單位長度和3個單位長度的速度同時相向移動,在點C相遇,求點C表示的數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校組織團員舉行申奧成功宣傳活動,從學校騎車出發,先上坡到達A地后,宣傳8分鐘;然后下坡到B地宣傳8分鐘返回,行程情況如圖.若返回時,上、下坡速度仍保持不變,在A地仍要宣傳8分鐘,那么他們從B地返回學校用的時間是( )

A. 45.2分鐘 B. 48分鐘 C. 46分鐘 D. 33分鐘
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在平面直角坐標系中如圖所示,
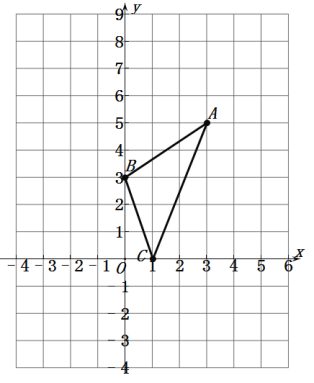
(1)S△ABC= .
(2)x軸上是否存在點P,使得S△BCP=2S△ABC,若不存在,說明理由;若存在,求出P點的坐標.
(3)請直接寫出:以A、B、C為頂點的平行四邊形的第四個頂點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學興趣小組活動中,小明進行數學探究活動.將邊長為2的正方形ABCD與邊長為3的正方形AEFG按圖1位置放置,AD與AE在同一條直線上,AB與AG在同一條直線上.
(1)小明發現DG=BE且DG⊥BE,請你給出證明.
(2)如圖2,小明將正方形ABCD繞點A逆時針旋轉,當點B恰好落在線段DG上時,請你幫他求出此時△ADG的面積.
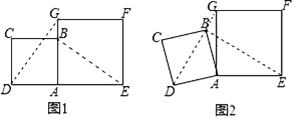
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知 a b , a 與b 兩個數在數軸上對應的點分別為點 A 、點 B ,求 A 、 B 兩點之間的距離.
(探索)
小明利用絕對值的概念,結合數軸,進行探索:

(1)補全小明的探索
(應用)
(2)若點C 對應的數c ,數軸上點C 到A、B 兩點的距離相等,求c .(用含a、b 的代數式表示)
(3)若點 D對應的數 d ,數軸上點 D 到 A 的距離是點 D 到 B 的距離的nn 0 倍,請探索 n 的取值范圍與點 D 個數的關系,并直接寫出a、b 、d、n 的關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com