
【題目】如圖,Rt△ABO的頂點A是反比例函數y=![]() 與一次函數y=﹣x﹣(k+1)的圖象在第二象限的交點,AB⊥x軸于B,且S△ABO=
與一次函數y=﹣x﹣(k+1)的圖象在第二象限的交點,AB⊥x軸于B,且S△ABO=![]() .
.
(1)直接寫出這兩個函數的關系式;
(2)求△AOC的面積;
(3)根據圖象直接寫出:當x為何值時,反比例函數的值小于一次函數的值.
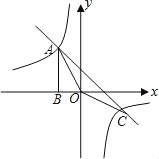
【答案】(1)y=![]() ;y=﹣x+2;(2)4;(3)x<﹣1或0<x<3時;
;y=﹣x+2;(2)4;(3)x<﹣1或0<x<3時;
【解析】
(1)先根據反比例函數的圖象所在的象限判斷出k的符號,在由△ABO的面積求出k的值,進而可得出兩個函數的解析式;
(2)把兩函數的解析式組成方程組,求出x、y的值,即可得出A、C兩點的坐標,再由一次函數的解析式求出直線與x軸的交點,由S△AOC=S△AOD+S△COD進行解答即可.
(3)直接根據一次函數與反比例函數的交點坐標求出一次函數的值大于反比例函數的值x的取值范圍即可.
解:(1)設點A(x,y),則xy=k
∵S△AOB=![]()
∴![]() (﹣x)×y=
(﹣x)×y=![]()
∴k=﹣3
∴反比例函數解析式y=![]()
一次函數解析式y=﹣x+2
(2)由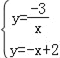
解得![]() ,
,![]()
∴A(﹣1,3)、C(3,﹣1)
∵一次函數y=﹣x+2與y軸的交點坐標為(0,2)
∴S△AOC=![]() ×2×(3+1)=4
×2×(3+1)=4
(3)由圖象可得:當x<﹣1或0<x<3時,一次函數圖象在反比例圖象的上方.


 步步高達標卷系列答案
步步高達標卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過原點O,頂點為A(1,1),且與直線y=x﹣2交于B,C兩點.
⑴求拋物線的解析式及點C的坐標;
⑵求證:△ABC是直角三角形;
⑶若點N為x軸上的一個動點,過點N作MN⊥x軸與拋物線交于點M,則是否存在以O,M,N為頂點的三角形與△ABC相似?若存在,請求出點N的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有以下命題:
①如果線段d是線段a,b,c的第四比例項,則有![]() ;
;
②如果點C是線段AB的中點,那么AC是AB.BC的比例中項;
③如果點C是線段AB的黃金分割點,且AC>BC,那么AC是AB與BC的比例中項;
④如果點C是線段AB的黃金分割點,AC>BC,且AB=2,則AC=![]() -1.
-1.
其中正確的判斷有( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,以斜邊AB為邊向外作正方形ABDE,且正方形對角線交于點O,連接OC,已知AC=![]() ,OC=
,OC=![]() ,則另一直角邊BC的長為__________.
,則另一直角邊BC的長為__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】點P是正方形ABCD邊AB上一點(不與A,B重合),連接PD并將線段PD繞點P順時針旋轉90°,得線段PE,連接BE,則∠CBE等于( )

A. 75° B. 60° C. 45° D. 30°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+3交x軸于A點,將一塊等腰直角三角形紙板的直角頂點置于原點O,另兩個頂點M、N恰落在直線y=
x+3交x軸于A點,將一塊等腰直角三角形紙板的直角頂點置于原點O,另兩個頂點M、N恰落在直線y=![]() x+3上,若N點在第二象限內,則tan∠AON的值為( )
x+3上,若N點在第二象限內,則tan∠AON的值為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
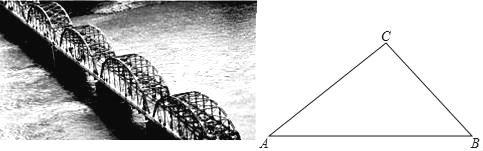
【題目】汾河孕育著世代的龍城子孫,而魅力汾河兩岸那“新外灘”的稱號,將太原人對汾河的愛表露無遺…貫穿太原的汾河,讓橋,也成為太原的文化符號,讓汾河兩岸,也成為繁華的必爭之地!北中環橋是世界上首座對稱五拱反對稱五跨非對稱斜拉索橋,2013年開工建設,當年實現全線竣工通車.這座橋造型現代,宛如一條騰飛巨龍.
小蕓和小剛分別在橋面上的A,B處,準備測量其中一座弧形鋼架拱梁頂部C處到橋面的距離AB=20m,小蕓在A處測得∠CAB=36°,小剛在B處測得∠CBA=43°,求弧形鋼架拱梁頂部C處到橋面的距離.(結果精確到0.1m)(參考數據sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某蔬菜生產基地用裝有恒溫系統的大棚栽培一種適宜生長溫度為15﹣20℃的新品種,如圖是某天恒溫系統從開啟到關閉及關閉后,大棚里溫度y(℃)隨時間x(h)變化的函數圖象,其中AB段是恒溫階段,BC段是雙曲線![]() 的一部分,請根據圖中信息解答下列問題:
的一部分,請根據圖中信息解答下列問題:
(1)求k的值;
(2)恒溫系統在一天內保持大棚里溫度在15℃及15℃以上的時間有多少小時?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場計劃從廠家購進甲、乙兩種不同型號的電視機,已知進價分別為:甲種每臺1500元,乙種每臺2100元.
(1)若商場同時購進這兩種不同型號的電視機50臺,金額不超過76000元,商場有幾種進貨方案,并寫出具體的進貨方案.
(2)在(1)的條件下,若商場銷售一臺甲、乙型號的電視機的銷售價分別為1650元、2300元,以上進貨方案中,哪種進貨方案獲利最多?最多為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com