
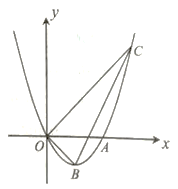
【題目】如圖,拋物線![]() 過原點,且與
過原點,且與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線的解析式及頂點![]() 的坐標;
的坐標;
(2)已知![]() 為拋物線上一點,連接
為拋物線上一點,連接![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)在第一象限的拋物線上是否存在一點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,使以
,使以![]() ,
,![]() ,
,![]() 三點為頂點的三角形與
三點為頂點的三角形與![]() 相似,若存在,求出滿足條件的點
相似,若存在,求出滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)拋物線的解析式為![]() ;頂點
;頂點![]() 的坐標為
的坐標為![]() ;(2)3;(3)
;(2)3;(3)![]() 點的坐標為
點的坐標為![]() 或
或![]() .
.
【解析】
(1)用待定系數法即可求出拋物線的解析式,進而即可求出頂點坐標;
(2)先將點C的橫坐標代入拋物線的解析式中求出縱坐標,根據B,C的坐標得出![]() ,
,![]() ,從而有
,從而有![]() ,最后利用
,最后利用![]() 求解即可;
求解即可;
(3)設![]() 為
為![]() .由于
.由于![]() ,所以當以
,所以當以![]() ,
,![]() ,
,![]() 三點為頂點的三角形與
三點為頂點的三角形與![]() 相似時,分兩種情況:
相似時,分兩種情況:![]() 或
或![]() ,分別建立方程計算即可.
,分別建立方程計算即可.
解:(1)∵拋物線![]() 過原點,且與
過原點,且與![]() 軸交于點
軸交于點![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴拋物線的解析式為![]() .
.
∵![]() ,
,
∴頂點![]() 的坐標為
的坐標為![]() .
.
(2)∵![]() 在拋物線上,
在拋物線上,
∴![]() .
.
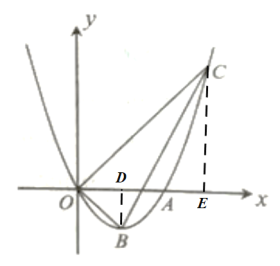
作![]() 軸于
軸于![]() ,作
,作![]() 軸于
軸于![]() ,
,
則![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,![]() .
.
∴![]() .
.
(3)假設存在.
設![]() 點的橫坐標為
點的橫坐標為![]() ,則
,則![]() 為
為![]() .
.
由于![]() ,
,
所以當以![]() ,
,![]() ,
,![]() 三點為頂點的三角形與
三點為頂點的三角形與![]() 相似時,
相似時,
有![]() 或
或![]()
∴ ![]() 或
或![]() .
.
解得![]() 或
或![]() .
.
∴存在點![]() ,使以
,使以![]() ,
,![]() ,
,![]() 三點為頂點的三角形與
三點為頂點的三角形與![]() 相似.
相似.
∴![]() 點的坐標為
點的坐標為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
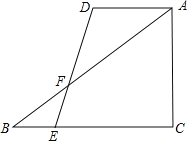
【題目】如圖,在Rt△ABC中,∠C=90°,AC=6,AD∥BC,DE與AB交于點F,已知AD=4,DF=2EF,sin∠DAB=![]() ,則線段DE=_____.
,則線段DE=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
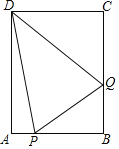
【題目】如圖,矩形ABCD中,AB=6cm,AD=8cm,點P從點A出發,以每秒一個單位的速度沿A→B→C的方向運動;同時點Q從點B出發,以每秒2個單位的速度沿B→C→D的方向運動,當其中一點到達終點后兩點都停止運動.設兩點運動的時間為t秒.
(1)當t= 時,兩點停止運動;
(2)設△BPQ的面積面積為S(平方單位)
①求S與t之間的函數關系式;
②求t為何值時,△BPQ面積最大,最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,已知
,已知![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 是
是![]() 上五點,
上五點,![]() 的直徑
的直徑![]() ,
,![]() .
.![]() 為
為![]() 的中點,延長
的中點,延長![]() 到點
到點![]() .使
.使![]() ,連接
,連接![]() .
.
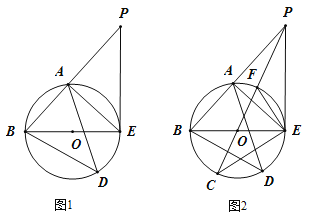
(1)求線段![]() 的長;
的長;
(2)求證:直線![]() 是
是![]() 的切線.
的切線.
(3)如圖![]() ,連
,連![]() 交
交![]() 于點
于點![]() ,延長交PO交
,延長交PO交![]() 于另一點
于另一點![]() ,連
,連![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線![]() 上部分點的橫坐標
上部分點的橫坐標![]() ,縱坐標
,縱坐標![]() 的對應值如下表:
的對應值如下表:
|
| -3 | -2 | -1 | 0 | 1 |
|
|
| 0 | 4 | 3 | 0 |
|
(1)把表格填寫完整;
(2)根據上表填空:
①拋物線與![]() 軸的交點坐標是________和__________;
軸的交點坐標是________和__________;
②在對稱軸右側,![]() 隨
隨![]() 增大而_______________;
增大而_______________;
③當![]() 時,則
時,則![]() 的取值范圍是_________________;
的取值范圍是_________________;
(3)請直接寫出拋物線![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學課外興趣活動小組準備圍建一個矩形苗圃,其中一邊靠墻,另外三邊用長為30米的籬笆圍成.已知墻長為18米(如圖所示),設這個苗圃垂直于墻的一邊長為x米.
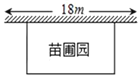
(1)若苗圃的面積為72平方米,求x的值;
(2)這個苗圃的面積能否是120平方米?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》記載“今有邑方不知大小,各中開門.出北門三十步有木,出西門七百五十步見木.問邑方有幾何?”意思是:如圖,點M、點N分別是正方形ABCD的邊AD、AB的中點,ME⊥AD,NF⊥AB,EF過點A,且ME=30步,NF=750步,則正方形的邊長為( )
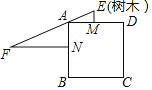
A. 150步B. 200步C. 250步D. 300步
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com