【題目】如圖，等邊△
中，
于
，
，點
、
分別為
、
上的兩個定點且
，在
上有一動點
使
最短，則的最小值為_____
.
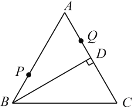
【答案】5
【解析】
作點Q關(guān)于BD的對稱點Q′，連接PQ′交BD于E，連接QE，此時PE+EQ的值最小，最小值PE+PQ=PE+EQ′=PQ′；
解：如圖，∵△ABC是等邊三角形，
∴BA=BC，
∵BD⊥AC，
∴AD=DC=3.5cm，
作點Q關(guān)于BD的對稱點Q′，連接PQ′交BD于E，連接QE，此時PE+EQ的值最小．最小值PE+PQ=PE+EQ′=PQ′，
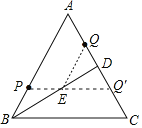
∵AQ=2cm，AD=DC=3.5cm，
∴QD=DQ′=1.5cm，
∴CQ′=BP=2cm，
∴AP=AQ′=5cm，
∵∠A=60°，
∴△APQ′是等邊三角形，
∴PQ′=PA=5cm，
∴PE+QE的最小值為：5cm．
故答案為：5．
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，拋物線
與
軸交于
，
兩點，與
軸交于點
，頂點為
，以
為直徑作
D．下列結(jié)論：①拋物線的對稱軸是直線x=3；②⊙D的面積為16π；③拋物線上存在點E，使四邊形ACED為平行四邊形；④直線CM與⊙D相切．其中正確結(jié)論的個數(shù)是（ ）
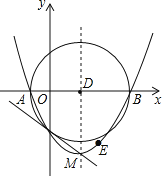
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖1，在平面直角坐標(biāo)系中，直線
與
軸，
軸分別交于
，
兩點，點
從點出發(fā)，沿射線
的方向運動，已知
，點的橫坐標(biāo)為，連接
，
，記
的面積為
.
（1）求關(guān)于的函數(shù)關(guān)系式及的取值范圍；
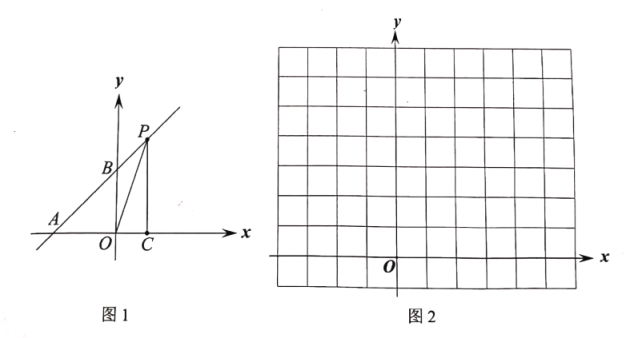
（2）在圖2所示的平面直角坐標(biāo)系中畫出（1）中所得函數(shù)的圖象，記其與軸的交點為
，將該圖象繞點逆時針旋轉(zhuǎn)
，畫出旋轉(zhuǎn)后的圖象；
（3）結(jié)合函數(shù)圖象，直接寫出旋轉(zhuǎn)前后的圖象與直線
的交點坐標(biāo).
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
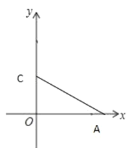
【題目】在直角坐標(biāo)系中，已知
、
，
，在
的邊上取兩點
、
（點是不同于點
的點），若以
、
、為頂點的三角形與
全等，則符合條件的點的坐標(biāo)為__________．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】某直銷公司現(xiàn)有
名推銷員，
月份每個人完成銷售額（單位：萬元），數(shù)據(jù)如下：
整理上面的數(shù)據(jù)得到如下統(tǒng)計表：
銷售額 |
|
|
|
|
|
|
|
|
|
|
人數(shù) |
|
|
|
|
|
|
|
|
|
|
（1）統(tǒng)計表中的
；
；
（2）銷售額的平均數(shù)是 ；眾數(shù)是 ；中位數(shù)是 .
（3）
月起，公司為了提高推銷員的積極性，將采取績效工資制度：規(guī)定一個基本銷售額，在基本銷售額內(nèi)，按
抽成；從公司低成本與員工愿意接受兩個層面考慮，你認(rèn)為基本銷售額定位多少萬元？請說明理由.
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知：直線
，點
，
分別是直線
，
上任意兩點，在直線上取一點
，使
，連接
，在直線上任取一點
，作
，
交直線于點
．
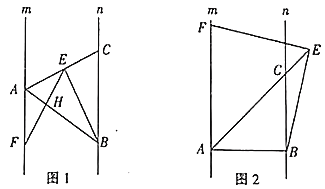
（1）如圖1，若點是線段上任意一點，交
于
，求證：
；
（2）如圖2，點在線段的延長線上時，
與
互為補角，若
，請判斷線段與
的數(shù)量關(guān)系，并說明理由．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
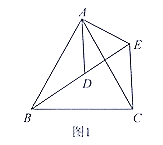
【題目】(1)問題發(fā)現(xiàn):如圖1, 
和
均為等邊三角形，點
在同一直線上，連接
①求證:
; ②求
的度數(shù).
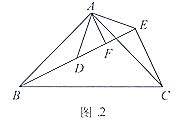
(2)拓展探究:如圖2, 
和均為等腰直角三角形，
,點在同一直線上
為中
邊上的高，連接
①求的度數(shù):
②判斷線段
之間的數(shù)量關(guān)系(直接寫出結(jié)果即可).
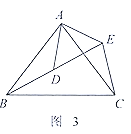
解決問題:如圖3，和均為等腰三角形，
,點在同一直線上，連接
.求
的度數(shù)(用含
的代數(shù)式表示，直接寫出結(jié)果即可).
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知點A（1，0），B（0，2），以AB為邊在第一象限內(nèi)作正方形ABCD，直線CD與y軸交于點G，再以DG為邊在第一象限內(nèi)作正方形DEFG，若反比例函數(shù)
的圖像經(jīng)過點E，則k的值是 （ ）
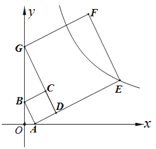
（A）33 （B）34 （C）35 （D）36
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】已知拋物線y=ax2+bx+c．
（Ⅰ）若拋物線的頂點為A（﹣2，﹣4），拋物線經(jīng)過點B（﹣4，0）
①求該拋物線的解析式；
②連接AB，把AB所在直線沿y軸向上平移，使它經(jīng)過原點O，得到直線l，點P是直線l上一動點．
設(shè)以點A，B，O，P為頂點的四邊形的面積為S，點P的橫坐標(biāo)為x，當(dāng)4+6
≤S≤6+8時，求x的取值范圍；
（Ⅱ）若a＞0，c＞1，當(dāng)x=c時，y=0，當(dāng)0＜x＜c時，y＞0，試比較ac與l的大小，并說明理由．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
