
【題目】在平面直角坐標系中,拋物線![]() 經過點
經過點![]() 和點
和點![]() .
.
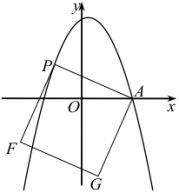
(1)求拋物線的解析式;
(2)![]() 為拋物線上的一個動點,點
為拋物線上的一個動點,點![]() 關于原點的對稱點為
關于原點的對稱點為![]() .當點
.當點![]() 落在該拋物線上時,求
落在該拋物線上時,求![]() 的值;
的值;
(3)![]()
![]() 是拋物線上一動點,連接
是拋物線上一動點,連接![]() ,以
,以![]() 為邊作圖示一側的正方形
為邊作圖示一側的正方形![]() ,隨著點
,隨著點![]() 的運動,正方形的大小與位置也隨之改變,當頂點
的運動,正方形的大小與位置也隨之改變,當頂點![]() 或
或![]() 恰好落在
恰好落在![]() 軸上時,求對應的
軸上時,求對應的![]() 點坐標.
點坐標.
【答案】(1)![]() .(2)
.(2)![]() 或
或![]() .(3)
.(3)![]() 點的坐標為
點的坐標為![]() ,
,![]() ,
,
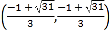 ,
,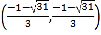 .
.
【解析】
(1)將![]() 和點
和點![]() 代入解析式解方程即可;
代入解析式解方程即可;
(2)將![]() 的坐標表示,把
的坐標表示,把![]() 坐標代入解析式求m即可;
坐標代入解析式求m即可;
(3)利用正方形性質和一線三直角幾何模型,找到全等三角形,根據直角邊解方程即可.
(1)∵拋物線![]() 經過點
經過點![]() 和點
和點![]() .
.
得![]() ,解得
,解得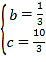
∴拋物線的解析式為![]() .
.
(2)∵![]() 與
與![]() 關于原點對稱,
關于原點對稱,
∴![]() 的坐標為
的坐標為![]() .
.
∵![]() ,
,![]() 都在拋物線
都在拋物線![]() 上,
上,
∴![]() ,
,![]() .
.
∴![]() .
.
解得![]() 或
或![]() .
.
(3)當點![]() 落在
落在![]() 軸上時,
軸上時,
如圖1,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,
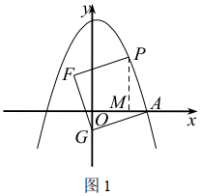
∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 點坐標為
點坐標為![]() .
.
如圖2,過點![]() 作
作![]() 軸于點
軸于點![]() ,
,
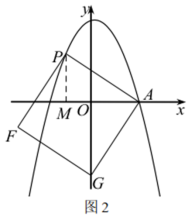
同理可以證得![]() ,
,
∴![]() .
.
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 點坐標為
點坐標為![]() .
.
當點![]() 落在
落在![]() 軸上時,
軸上時,
如圖3,過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,
,
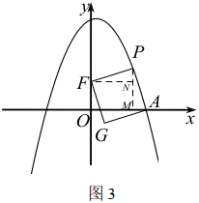
同理可以證得![]() ,
,
∴![]() ,
,
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 點坐標為
點坐標為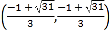 .
.
如圖4,過點![]() 作
作![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 的延長線于點
的延長線于點![]() ,
,
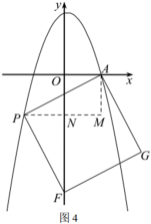
同理可以證得![]() ,
,
∴![]() ,
,
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 點坐標為
點坐標為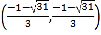 .
.
綜上所述,![]() 點的坐標為
點的坐標為![]() ,
,![]() ,
,
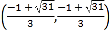 ,
,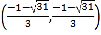 .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,直線![]() (k為常數)與拋物線
(k為常數)與拋物線![]() 交于A,B兩點,且A點在
交于A,B兩點,且A點在![]() 軸右側,P點的坐標為(0,4)連接PA,PB.(1)△PAB的面積的最小值為____;(2)當
軸右側,P點的坐標為(0,4)連接PA,PB.(1)△PAB的面積的最小值為____;(2)當![]() 時,
時,![]() =_______
=_______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC為⊙O的內接三角形,AB為⊙O的直徑,將△ABC沿直線AB折疊得到△ABD,交⊙O于點D.連接CD交AB于點E,延長BD和CA相交于點P,過點A作AG∥CD交BP于點G.
(1)求證:直線GA是⊙O的切線;
(2)求證:AC2=GDBD;
(3)若tan∠AGB=![]() ,PG=6,求cos∠P的值.
,PG=6,求cos∠P的值.
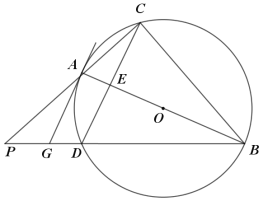
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點E是邊BC上任意一點(點E不與點B、C重合),連結DE,點C關于DE的對稱點為C1,連結AC1并延長交DE的延長線于點M,F是AC1的中點,連結DF.
(猜想)如圖①,∠FDM的大小為 度.
(探究)如圖②,過點A作AM1∥DF交MD的延長線于點M1,連結BM.求證:△ABM≌△ADM1.
(拓展)如圖③,連結AC,若正方形ABCD的邊長為2,則△ACC1面積的最大值為 .
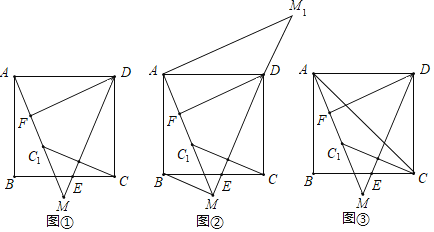
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在每個小正方形的邊長為1的網格中,![]() ,
,![]() ,
,![]() 為格點,
為格點,![]() 為小正方形邊的中點.
為小正方形邊的中點.
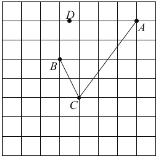
(1)![]() 的長等于_________;
的長等于_________;
(2)點![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 上的動點,當
上的動點,當![]() 取得最小值時,請在如圖所示的網格中,用無刻度的直尺,畫出線段
取得最小值時,請在如圖所示的網格中,用無刻度的直尺,畫出線段![]() ,
,![]() ,并簡要說明點
,并簡要說明點![]() 和點
和點![]() 的位置是如何找到的(不要求證明).
的位置是如何找到的(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1個單位長度的小正方形組成的網格中,給出了格點![]() (頂點是網格線的交點)和直線l及點O.
(頂點是網格線的交點)和直線l及點O.
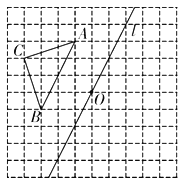
(1)畫出![]() 關于直線l對稱的
關于直線l對稱的![]() ;
;
(2)連接OA,將OA繞點O順時針旋轉![]() ,畫出旋轉后的線段;
,畫出旋轉后的線段;
(3)在旋轉過程中,當OA與![]() 有交點時,旋轉角
有交點時,旋轉角![]() 的取值范圍為________.
的取值范圍為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在全球關注的抗擊“新冠肺炎”中某跨國科研中心的一個團隊研制了一種助治“新冠附炎”的新藥,在試驗藥效時發現,如果成人按規定的制量服用,那么服藥后2小時血液中含藥量最高,達每毫升8微克(1微克=![]() 毫克),接著逐步安減,10小時時血液中含藥最為每毫升3微克,每毫升血液中含藥量
毫克),接著逐步安減,10小時時血液中含藥最為每毫升3微克,每毫升血液中含藥量![]() (微克)隨時間
(微克)隨時間![]() (小時)的變化如圖所示.
(小時)的變化如圖所示.
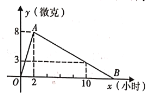
(1)分別求線段![]() 所表示的函數關系式;
所表示的函數關系式;
(2)如果每毫升血液中含藥量為4微克或4微克以上時對治病是有效的,那么這個有效時間是多長?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學的一個數學興趣小組在本校學生中開展了主題為“霧霾知多少”的專題調查括動,采取隨機抽樣的方式進行問卷調查,問卷調查的結果分為“A.非常了解”、“B.比較了解”、“C.基本了解”、“D.不太了解”四個等級,將所得數據進行整理后,繪制成如下兩幅不完整的統計圖表,請你結合圖表中的信息解答下列問題
等級 | A | B | C | D |
頻數 | 40 | 120 | 36 | n |
頻率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形統計圖中,A部分所對應的扇形的圓心角是 °,所抽取學生對丁霧霾了解程度的眾數是 ;
(3)若該校共有學生1500人,請根據調查結果估計這些學生中“比較了解”人數約為多少?
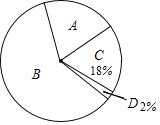
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com