
【題目】如圖1,A,B分別在射線OA,ON上,且∠MON為鈍角,現以線段OA,OB為斜邊向∠MON的外側作等腰直角三角形,分別是△OAP,△OBQ,點C,D,E分別是OA,OB,AB的中點.
(1)求證:△PCE≌△EDQ;
(2)延長PC,QD交于點R.如圖2,若∠MON=150°,求證:△ABR為等邊三角形;
(3)如圖3,若△ARB∽△PEQ,求∠MON大小
【答案】
(1)證明:∵點C、D、E分別是OA,OB,AB的中點,
∴DE=OC,∥OC,CE=OD,CE∥OD,
∴四邊形ODEC是平行四邊形,
∴∠OCE=∠ODE,
∵△OAP,△OBQ是等腰直角三角形,
∴∠PCO=∠QDO=90°,
∴∠PCE=∠PCO+∠OCE=∠QDO=∠ODQ=∠EDQ,
∵PC= ![]() AO=OC=ED,CE=OD=
AO=OC=ED,CE=OD= ![]() OB=DQ,
OB=DQ,
在△PCE與△EDQ中,
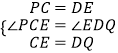 ,
,
∴△PCE≌△EDQ;
(2)解:如圖2,連接RO,
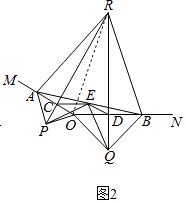
∵PR與QR分別是OA,OB的垂直平分線,
∴AP=OR=RB,
∴∠ARC=∠ORC,∠ORQ=∠BRO,
∵∠RCO=∠RDO=90°,∠COD=150°,
∴∠CRD=30°,
∴∠ARB=60°,
∴△ARB是等邊三角形;
(3)解:如圖3中,

由(1)得,EQ=EP,∠DEQ=∠CPE,
∴∠PEQ=∠CED﹣∠CEP﹣∠DEQ=∠ACE﹣∠CEP﹣∠CPE=∠ACE﹣∠RCE=∠ACR=90°,
∴△PEQ是等腰直角三角形,
∵△ARB∽△PEQ,
∴∠ARB=∠PEQ=90°,
∴∠OCR=∠ODR=90°,∠CRD= ![]() ∠ARB=45°,
∠ARB=45°,
∴∠MON=180°﹣∠CRD=135°.
【解析】(1)此小題關鍵是根據三角形的中位線的性質得到得出四邊形ODEC是平行四邊形,于是得到∠OCE=∠ODE,根據等腰直角三角形得到∠PCO=∠QDO=90°,PC=ED,CE=DQ,即可得到結論;
(2)連接RO,由垂直平分線的性質,得到AP=OR=RB,再由等腰三角形的性質得到∠ARC=∠ORC,∠ORQ=∠BRO,在四邊形CRDO中得到∠CRD=30°,即可得到結論;
(3)由(1)得EQ=EP,∠DEQ=∠CPE,推出∠PEQ=∠ACR=90°,證得△PEQ是等腰直角三角形,根據相似三角形的性質得到∠ARB=∠PEQ=90°,從而求得∠MON的度數.
【考點精析】通過靈活運用平行四邊形的判定與性質和相似三角形的判定與性質,掌握若一直線過平行四邊形兩對角線的交點,則這條直線被一組對邊截下的線段以對角線的交點為中點,并且這兩條直線二等分此平行四邊形的面積;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方即可以解答此題.


 作業輔導系列答案
作業輔導系列答案科目:初中數學 來源: 題型:
【題目】如圖,某翼裝飛行員從離水平地面高AC=500m的A處出發,沿著俯角為15°的方向,直線滑行1600米到達D點,然后打開降落傘以75°的俯角降落到地面上的B點.求他飛行的水平距離BC(結果精確到1m).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為某城市部分街道示意圖,四邊形ABCD為正方形,點G在對角線BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路線為B→A→G→E,小聰行走的路線為B→A→D→E→F.若小敏行走的路程為3100m,則小聰行走的路程為 m.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據調查,超速行駛是引發交通事故的主要原因之一,所以規定以下情境中的速度不得超過15m/s,在一條筆直公路BD的上方A處有一探測儀.如圖,AD=24m,∠D=90°,第一次探測到一輛轎車從B點勻速向D點行駛,測得∠ABD=31°,2秒后到達C點,測得∠ACD=50°
(1)求B,C的距離.
(2)通過計算,判斷此轎車是否超速.(tan31°≈0.6,tan50°≈1.2,結果精確到1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1.平面直角坐標系![]() 為原點,長方形
為原點,長方形![]() 的頂點
的頂點![]() 在坐標軸上,點
在坐標軸上,點![]() ,
,![]() ,且己知
,且己知![]() 是64的立方根,
是64的立方根,![]() .
.
(1)求點![]() 的坐標;
的坐標;
(2)如圖1,有兩動點![]() 點從
點從![]() 點出發沿
點出發沿![]() 軸負方向以1個單位長度每秒的速度勻速移動,
軸負方向以1個單位長度每秒的速度勻速移動,![]() 點從
點從![]() 點出發以2個單位長度每秒的速度沿
點出發以2個單位長度每秒的速度沿![]() 的路線勻速移動,
的路線勻速移動,![]() 點到達
點到達![]() 點整個運動隨之結束.若長方形對角線
點整個運動隨之結束.若長方形對角線![]() 的交點
的交點![]() 的坐標是
的坐標是![]() ,設運動時間為
,設運動時間為![]() 秒,問:以
秒,問:以![]() 為頂點的多邊形面積是否為定值,若是,請求出此多邊形的面積;若不是,請說明理由.
為頂點的多邊形面積是否為定值,若是,請求出此多邊形的面積;若不是,請說明理由.
(3)如圖2,![]() 是線段
是線段![]() 上一點,使
上一點,使![]() ,點
,點![]() 是線段
是線段![]() 上任意一點(
上任意一點(![]() 不與點
不與點![]() 重合),連接
重合),連接![]() 交
交![]() 于點
于點![]() .已知
.已知![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,某數學活動小組選定測量小河對岸大樹BC的高度,他們在斜坡上D處測得大樹頂端B的仰角是30°,朝大樹方向下坡走6米到達坡底A處,在A處測得大樹頂端B的仰角是48°,若坡角∠FAE=30°,求大樹的高度(結果保留整數,參考數據:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11, ![]() ≈1.73)
≈1.73)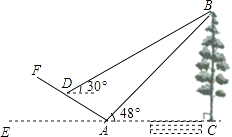
查看答案和解析>>
科目:初中數學 來源: 題型:
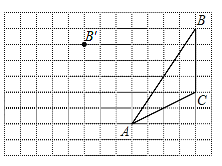
【題目】畫圖并填空:如圖,方格紙中每個小正方形的邊長都為 1,在方格紙內將△ABC經過一次平移后得到△A′B′C′,圖中標出了點B 的對應點 B′.
(1)在給定方格紙中畫出平移后的△A′B′C′;
(2)線段 AA′與線段 BB′的數量和位置關系是___________;
(3)求△A′B′C′的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com