
【題目】如圖,在平面直角坐標系中,點A,B的坐標分別為(﹣1,0),(3,0),現同時將點A,B,分別向上平移2個單位,再向右平移1個單位,分別得到點A、B的對應點C、D,連接AC,BD,CD,得平行四邊形ABDC.
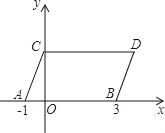
(1)直接寫出點C,D的坐標;
(2)若在直線CD上存在點M,連接MA,MB,使S△MAB=2S△MBD,求出點M的坐標;
(3)若點P在直線BD上運動,連接PC,PO,請畫出圖形,寫出∠CPO,∠DCP,∠BOP的數量關系,并說明理由.
【答案】(1)C(0,2),D(4,2);(2)M(2,2)或(6,2);(3)①當點P在BD上,∠CPO=∠DCP+∠BOP,見解析;②當點P在線段BD的延長線上時,∠CPO=∠BOP﹣∠DCP,見解析;③當點P在線段DB的延長線上時,∠CPO=∠DCP﹣∠BOP,見解析.
【解析】
(1)根據向上平移縱坐標加,向右平移橫坐標加求出點C、D的坐標即可,
(2)先求出S△MAB=4,進而判斷出SABCD=2S△MAB=2S△BCD,進而判斷出S△MBD=2,再分兩種情況即可得出結論;
(3)分三種情況,根據平移的性質可得AB∥CD,再過點P作PE∥AB,根據平行公理可得PE∥CD,然后根據兩直線平行,內錯角相等可得∠DCP=∠CPE,∠BOP=∠OPE即可得出結論.
解:(1)∵將A(﹣1,0),B(3,0)分別向上平移2個單位,再向右平移1個單位,
∴C(0,2),D(4,2);
(2)∵AB=4,CO=2,
∴S△MAB=![]() AB×OC=4,
AB×OC=4,
∵SABCD=AB×OC=8=2S△MAB=2S△BCD,
∵S△MAB=2S△MBD,
∴S△MBD=2,
當點M在邊CD上時,
∴點M是CD的中點,
∴M(2,2),
當點M在CD的延長線上時,
利用對稱性得,M'(6,2),
∴M(2,2)或(6,2);
(3)①當點P在BD上,如圖1,
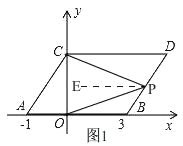
由平移的性質得,AB∥CD,
過點P作PE∥AB,則PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
②當點P在線段BD的延長線上時,如圖2,
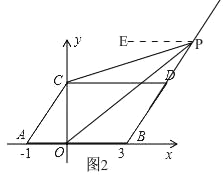
由平移的性質得,AB∥CD,
過點P作PE∥AB,則PE∥CD,
∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠OPE﹣∠CPE=∠BOP﹣∠DCP,
③當點P在線段DB的延長線上時,如圖3,
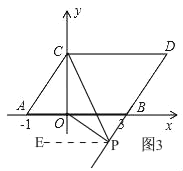
同(2)的方法得出∠CPO=∠DCP﹣∠BOP.


科目:初中數學 來源: 題型:
【題目】臨近端午節,某食品店每天賣出300只粽子,賣出一只粽子的利潤為1元.經調查發現,零售單價每降0.1元,每天可多賣出100只粽子.為了使每天獲得的利潤更多,該店決定把零售單價下降m(0<m<1)元,
(1)零售單價降價后,每只利潤為 元,該店每天可售出 只粽子.
(2)在不考慮其他因素的條件下,當零售單價下降多少元時,才能使該店每天獲取的利潤是420元,且賣出的粽子更多?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業用規格是170×40的標準板材作為原材料,按照如圖1所示的裁法一或裁法二,裁剪出甲型與乙型兩種板材(單位:cm)

(1)求圖中a,b的值;
(2)若將50張標準板材按裁法一裁剪,10張標準板材按裁法二裁剪,裁剪后將得到的甲型與乙型板材做側面或底面,做成如圖2的豎式與橫式兩種無蓋的裝飾盒若干(接縫處的長度忽略不計).

①一共可裁剪出甲型板材______張,乙型板材______張;
②設可以做出豎式和橫式兩種無蓋裝飾盒一共x個,則x的最大值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷一種雙肩包,已知這種雙肩包的成本價為每個30元.市場調查發現,這種雙肩包每天的銷售量y(單位:個)與銷售單價x(單位:元)有如下關系:y=﹣x+60(30≤x≤60).設這種雙肩包每天的銷售利潤為w元.
(1)求w與x之間的函數解析式;
(2)這種雙肩包銷售單價定為多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)如果物價部門規定這種雙肩包的銷售單價不高于48元,該商店銷售這種雙肩包每天要獲得200元的銷售利潤,銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市一山區學校為部分家遠的學生安排住宿,將部分教室改造成若干間住房. 如果每間住5人,那么有12人安排不下;如果每間住8人,那么有一間房還余一些床位,問該校可能有幾間住房可以安排學生住宿?住宿的學生可能有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為弘揚中華民族傳統文化,某校舉辦了“古詩文大賽”,并為獲獎同學購買簽字筆和筆記本作為獎品.1支簽字筆和2個筆記本共8.5元,2支簽字筆和3個筆記本共13.5元.
(1)求簽字筆和筆記本的單價分別是多少元?
(2)為了激發學生的學習熱情,學校決定給每名獲獎同學再購買一本文學類且定價為15元的圖書.書店出臺如下促銷方案:購買圖書總數超過50本可以享受8折優惠,學校如果多買12本,則可以享受優惠且所花錢數與原來相同,問學校獲獎的同學有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
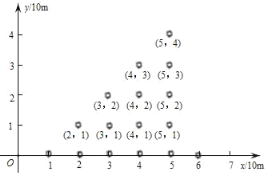
【題目】某景區有一片樹林,不僅樹種相同,而且排列有序,如果用平面直角坐標系來表示每一棵的具體位置,從第一棵樹開始依次表示為(1,0)→(2,0)→(2,1)→(3,2)→(3,1)→(3,0)→(4.0)→……,則第100棵樹的位置是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與實踐:
問題發現:學完四邊形的有關知識后,創新小組的同學進一步研究特殊的四邊形,發現了一個結論.如圖1,已知四邊形![]() 是正方形,根據勾股定理和正方形的性質,很容易能夠證明
是正方形,根據勾股定理和正方形的性質,很容易能夠證明![]() .
.
問題探究:
(1)如圖2,已知四邊形![]() 是矩形,若
是矩形,若![]() ,則
,則![]() 的值是 ;
的值是 ;![]() 的值是 ;
的值是 ;
(2)如圖3,已知四邊形![]() 是菱形,證明:
是菱形,證明:![]() ;
;
拓廣探索:
(3)智慧小組看了創新小組交流后,提出了一個猜想,如圖4,在![]() 中,
中,![]() ,你認為這個猜想正確嗎?請說明理由;
,你認為這個猜想正確嗎?請說明理由;
(4)請用文字語言敘述![]() 中得出的結論.
中得出的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面的證明過程.
如圖,已知,∠1+∠2=180°,∠A=∠D.求證AB∥CD.
證明:∵∠1+∠2=180°(已知)
∠1=∠3( )
∴∠3+∠2=180°( )
∴AE∥ ( )
∴∠D= ( )
∵∠A=∠D(已知)
∴∠A=∠CEA( )
∴AB∥CD ( )

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com