
【題目】已知:如圖,四邊形ABCD是邊長為1的正方形,對角線AC、BD相交于點O.過點O作一直角∠MON,直角邊OM、ON分別與OA、OB重合,然后逆時針旋轉∠MON,旋轉角為θ(0°<θ<90°),OM、ON分別交AB、BC于E、F兩點,連接EF交OB于點G,則下列結論中正確的是________(填序號).
①![]() ;②S四邊形OEBF:S正方形ABCD=1:2;③
;②S四邊形OEBF:S正方形ABCD=1:2;③![]() ;④OGBD=AE2+CF2;⑤在旋轉過程中,當△BEF與△COF的面積之和最大時,
;④OGBD=AE2+CF2;⑤在旋轉過程中,當△BEF與△COF的面積之和最大時,![]() .
.
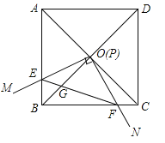
【答案】①③④
【解析】
①②③證明△BOE≌△COF,結合正方形的性質可判斷;④證明![]() ,結合△BOE≌△COF的性質即可證得;⑤作OH⊥BC,表示出S△BEF+S△COF,即可判斷.
,結合△BOE≌△COF的性質即可證得;⑤作OH⊥BC,表示出S△BEF+S△COF,即可判斷.
①∵四邊形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
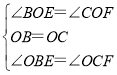 ,
,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF=![]() OE;故①正確;
OE;故①正確;
②∵S四邊形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴S四邊形OEBF:S正方形ABCD=1:4;故②錯誤;
③∴BE+BF=BF+CF=BC=![]() OA;故③正確;
OA;故③正確;
④∵![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∵在![]() 中,
中,![]()
∴![]()
∴![]() ,故④正確;
,故④正確;
⑤過點O作OH⊥BC,
∵BC=1,
∴OH=![]() BC=
BC=![]() ,
,
設AE=![]() ,則BE=CF=1-
,則BE=CF=1-![]() ,BF=
,BF=![]() ,
,
∴S△BEF+S△COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]()
![]() (1-
(1-![]() )+
)+![]() (1-
(1-![]() )×
)×![]() =-
=-![]() (
(![]() -
-![]() )2+
)2+![]() ,
,
∵![]() <0,
<0,
∴當![]() =
=![]() 時,S△BEF+S△COF最大;
時,S△BEF+S△COF最大;
即在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=![]() ;故⑤錯誤;
;故⑤錯誤;
故答案為①③④.


科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=8,BC=12,E為AD中點,F為AB上一點,將△AEF沿EF折疊后,點A恰好落到CF上的點G處,則折痕EF的長是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】人類的血型一般可分為A,B,AB,O型四種,寧波市中心血戰2015年共有8萬人無償獻血,血戰統計人員由電腦隨機選出20人,血型分別是:
O,A,O,B,O,A,A,AB,A,O,O,B,AB,B,O,A,O,B,O,A.
(1)請設計統計表分類統計這20人各類血型人數;
(2)若每位獻血者平均獻血200毫升,一年中寧波市各醫院O型血用血量約為6×106毫米,請你估計2015年這8萬人所獻的O型血是否夠用?
查看答案和解析>>
科目:初中數學 來源: 題型:
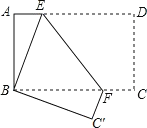
【題目】如圖,長方形紙片 ABCD,AD∥BC,將長方形紙片折疊, 使點 D 與點 B 重合,點 C 落在點 C'處,折痕為 EF.
(1)求證:BE=BF.
(2)若∠ABE=18°,求∠BFE 的度數.
(3)若 AB=4,AD=8,求 AE 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠A=∠B=30°,過點C作CD⊥AC,交AB于點D.
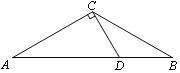
(1)作⊙O,使⊙O經過A、C、D三點(尺規作圖,保留作圖痕跡,不寫作法);
(2)判斷直線 BC與⊙O的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學習了相似三角形的知識后,愛探究的小明下晚自習后利用路燈的光線去測量了一路燈的高度,并作出了示意圖:如圖,路燈(點P)距地面若干米,身高1.6米的小明站在距路燈的底部(O點)20米的A點時,身影的長度AM為5米;
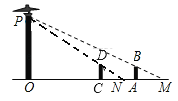
(1)請幫助小明求出路燈距地面的高度;
(2)若另一名身高為1.5米小龍站在直線OA上的C點時,測得他與小明的距離AC為7米,求小龍的身影的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
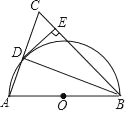
【題目】如圖,在△ABC中,BA=BC,以AB為直徑作⊙O,交AC于點D,連接DB,過點D作DE⊥BC,垂足為E.
(1)求證:AD=CD.
(2)求證:DE為⊙O的切線.
(3)若∠C=60°,DE=![]() ,求⊙O半徑的長.
,求⊙O半徑的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
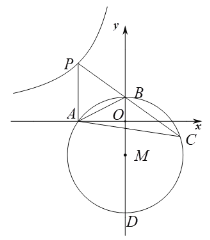
【題目】如圖,點![]() 在反比例函數
在反比例函數![]() 上,
上,![]() 軸于點
軸于點![]() ,點
,點![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() ,
,![]() 、
、![]() 的長是方程
的長是方程![]() 的兩個實數根,且
的兩個實數根,且![]() ,點
,點![]() 是線段
是線段![]() 延長線上的一個動點,
延長線上的一個動點,![]() 的外接圓
的外接圓![]() 與
與![]() 軸的另一個交點是
軸的另一個交點是![]() .
.
(1)求點![]() 和點
和點![]() 的坐標;
的坐標;
(2)求反比例函數的解析式;
(3)連接![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,![]() //
//![]() ,且分別交對角線AC于點E,F,連接BE,DF.
,且分別交對角線AC于點E,F,連接BE,DF.
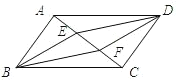
(1)求證:AE=CF;
(2)若BE=DE,求證:四邊形EBFD為菱形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com