【題目】下列運算正確的是（ ）
A.
﹣ 
=
B.
=﹣3
C.a?a2=a2
D.（2a3）2=4a6
名校練考卷期末沖刺卷系列答案科目：初中數學 來源： 題型：
【題目】某地為了鼓勵居民節約用水，決定實行兩級收費制，即每月用水量不超過15噸(含15噸)時，每噸按政府補貼優惠價收費；每月超過15噸時，超過部分每噸按市場調節價收費．小明家1月份用水23噸，交水費35元，2月份用水19噸，交水費25元．
(1)求每噸水的政府補貼優惠價與市場調節價分別是多少；
(2)小明家3月份用水24噸，他家應交水費多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有一快遞小哥騎電動車需要在規定的時間把快遞送到某地，若他以
的速度行駛就會提前2分鐘到達，如果他以
的速度行駛就要遲到6分鐘。
（1）快遞小哥行駛的路程是多少千米；
（2）當快遞小哥以的速度行駛10分鐘后，因某段路擁堵耽誤了3分鐘，為了剛好在規定時間到達，快遞小哥應以怎祥的速度行駛。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一架飛機在兩城之間飛行，風速為24千米/小時，順風飛行需2小時50分，逆風飛行需要3小時．
(1)求無風時飛機的飛行速度；
(2)求兩城之間的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某地在山區修建高速公路時需挖通一條隧道，為估計這條隧道的長度需測出這座山A、B間的距離，結合所學知識或方法，設計測量方案你能給出什么好的方法嗎？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知OA⊥OB，∠AOD=∠BOC由此判定OC⊥OD，下面是推理過程，請填空.
解：∵OA⊥OB(已知)
所以_____=90°（________）
因為_____=∠AOD-∠AOC，____=∠BOC-∠AOC，∠AOD=∠BOC，
所以______=_____(等量代換)
所以______=90°
所以OC⊥OD.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD為平行四邊形，E為BC的中點，連接AE并延長交DC的延長線于點F．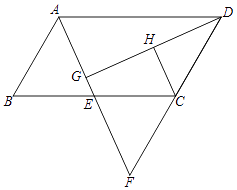 
（1）求證：△ABE≌△FCE；
（2）過點D作DG⊥AE于點G，H為DG的中點．判斷CH與DG的位置關系， 并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知直線l與⊙O相離，OA⊥l于點A，交⊙O于點P，點B是⊙O上一點，連接BP并延長，交直線l于點C，使得AB=AC．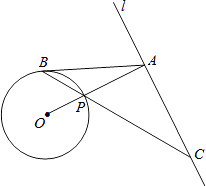 
（1）求證：AB是⊙O的切線；
（2）PC=2 
，OA=4． ①求⊙O的半徑；
②求線段PB的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
