【題目】如圖，一圓弧形橋拱的圓心為
，拱橋的水面跨度
米，橋拱到水面的最大高度
為
米．求：
橋拱的半徑；
現水面上漲后水面跨度為
米，求水面上漲的高度為________米．
【答案】(1)50;(2)10.
【解析】
（1）根據垂徑定理和勾股定理求解；
（2）由垂徑定理求出MH，由勾股定理求出EH，得出HF即可．
（1）如圖，
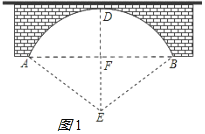
設點E是拱橋所在的圓的圓心，作EF⊥AB于F，延長EF交圓于點D，
則由垂徑定理知，點F是AB的中點，AF=FB=
AB=40，EF=ED-FD=AE-DF，
由勾股定理知，AE2=AF2+EF2=AF2+（AE-DF）2，
設圓的半徑是r，
則：r2=402+（r-20）2，
解得：r=50；
即橋拱的半徑為50米；
（2）設水面上漲后水面跨度MN為60米，MN交ED于H，連接EM，如圖2所示
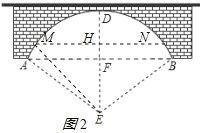
則MH=NH=MN=30，
∴EH=
=40（米），
∵EF=50-20=30（米），
∴HF=EH-EF=10（米）；
故答案為：10．
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y=
x2+bx+c的圖象交x軸于A、D兩點，并經過B點，已知A點坐標是（2，0），B點坐標是（8，6）．
（1）求二次函數的解析式；
（2）求函數圖象的頂點坐標及D點的坐標；
（3）二次函數的對稱軸上是否存在一點C，使得△CBD的周長最小？若C點存在，求出C點的坐標；若C點不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】大學生小韓在暑假創業，銷售一種進價為
元/件的玩具熊，銷售過程中發現，每周銷售量少（件）與銷售單價
（元）之間的關系可近似的看作一次函數：
如果小韓想要每周獲得
元的利潤，那么銷售單價應定為多少元？
設小韓每周獲得利潤為
（元），當銷售單價定為多少元時，每周可獲得利潤最大，最大利潤是多少？
若該玩具熊的銷售單價不得高于
元，如果小韓想要每周獲得的利潤不低于元，那么他的銷售單價應定為多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】A表示一個數，若把數A寫成形如
的形式，其中
、
、
、
、…都為整數．則我們稱把數A寫成連分數形式．
例如：把2.8寫成連分數形式的過程如下：
2.8-2=0.8，
，
1.25-1=0.25，
，
4-4=0．
（1）把3.245寫成連分數形式不完整的過程如下：
3.245-3=0.245，
，
4.082-4=0.082，
，
12.250-12=0.25，，
4-4=0．
∴
則
_____________；
_____________；
（2）請把
寫成連分數形式；
（3）有這樣一個問題：如圖是長為47，寬為10的長方形紙片．從中裁剪出正方形，若長方形紙片無剩余，則剪出的正方形最少是幾個？
小明認為這個問題和 “把一個數化為連分數形式” 有關聯，并把
化成連分數從而解決了問題．你可以參考小明的思路解決上述問題，請直接寫出“剪出的正方形最少”時，正方形的個數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】數學課上，張老師舉了下面的例題：
例1 等腰三角形
中，
，求
的度數.（答案：
）
例2 等腰三角形中，
，求的度數.（答案：
或
或
）
張老師啟發同學們進行變式，小敏編了如下兩題：
變式1: 等腰三角形中，∠A=100°，求的度數.
變式2: 等腰三角形中，∠A= 45° ，求的度數.
（1）請你解答以上兩道變式題.
（2）解（1）后，小敏發現，
的度數不同，得到的度數的個數也可能不同.如果在等腰三角形中，設
，當只有一個度數時，請你探索
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下列說法中，正確的是（ ）
A. “明天降雨的概率是
”表示明天有的時間降雨
B. “明天降雨的概率是”表示明天降雨的可能性有八成
C. “拋一枚硬幣正面朝上的概率是
”表示每拋硬幣
次就有
次出現正面朝上
D. “彩票中獎的概率是
”表示買
張彩票一定有張會中獎
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
