
【題目】在平面直角坐標系中,點P(a-4,2b+2),當a,b分別滿足什么條件時:
(1)點P在第一象限?
(2)點P在第四象限?
(3)點P在x軸上?
(4)點P在y軸上?
(5)點P在x軸下方?
(6)點P在y軸左側?
【答案】(1) ![]() (2)
(2) ![]() (3) b=-1.(4) a=4.(5) b<-1.(6) a<4.
(3) b=-1.(4) a=4.(5) b<-1.(6) a<4.
【解析】試題分析:象限內點![]() 的坐標特征為:
的坐標特征為:
第一象限(+,+),即![]()
第二象限(-,+),即![]()
第三象限(-,-),即![]()
第四象限(+,-),即![]()
坐標軸上點![]() 的坐標特征為
的坐標特征為![]() 軸上的點,縱坐標為零,
軸上的點,縱坐標為零, ![]() 軸上的點,橫坐標為零.
軸上的點,橫坐標為零.
反過來也成立.
![]() 軸下方的點,縱坐標小于零;
軸下方的點,縱坐標小于零; ![]() 軸左側的點,橫坐標小于零.
軸左側的點,橫坐標小于零.
試題解析:(1)當點![]() 在第一象限時,則橫坐標大于0,縱坐標大于0,則有
在第一象限時,則橫坐標大于0,縱坐標大于0,則有
![]() 且
且![]()
解得: ![]() 且
且![]()
所以點![]() 在第一象限時
在第一象限時![]() 且
且![]()
(2)當點![]() 在第四象限時,則橫坐標大于0,縱坐標小于0,則有
在第四象限時,則橫坐標大于0,縱坐標小于0,則有
![]() 且
且![]()
解得: ![]() 且
且![]()
所以點![]() 在第四象限時
在第四象限時![]() 且
且![]()
(3)當點![]() 在
在![]() 軸上時,則縱坐標為0,故有
軸上時,則縱坐標為0,故有
![]()
解得: ![]()
所以點![]() 在
在![]() 軸上時
軸上時![]()
(4)當點![]() 在
在![]() 軸上時,則橫坐標為0,故有
軸上時,則橫坐標為0,故有
![]()
解得: ![]()
所以當點![]() 在
在![]() 軸上時
軸上時![]()
(5)當點![]() 在
在![]() 軸下方時,則縱坐標小于0,則有
軸下方時,則縱坐標小于0,則有
![]()
解得: ![]()
所以當點![]() 在
在![]() 軸下方時
軸下方時![]()
(6)點在
![]() 軸的左側時,則橫坐標小于0,則有
軸的左側時,則橫坐標小于0,則有
![]()
解得: ![]()
所以當點![]() 在
在![]() 軸的左側時
軸的左側時![]()


科目:初中數學 來源: 題型:
【題目】某商場銷售甲、乙兩種品牌的智能手機,甲品牌手機的進價是4000元/部,售價為4300元/部,乙品牌的售價進價是2500元/部,售價為3000元/部,該商場計劃購進兩種手機若干部,共需15.5萬元,預計全部銷售后可獲毛利潤共2.1萬元,該商場計劃購進甲、乙兩種手機各多少部?(毛利潤=(售價﹣進價)×銷售量)
查看答案和解析>>
科目:初中數學 來源: 題型:
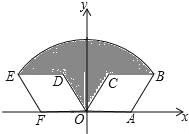
【題目】如圖,菱形OABC的頂點A的坐標為(2,0),∠COA=60°,將菱形OABC繞坐標原點O逆時針旋轉120°得到菱形ODEF,則線段OB= ;圖中陰影部分的面積為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com