
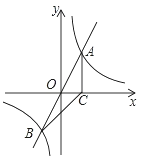
【題目】如圖,正比例函數![]() 的圖像與反比例函數
的圖像與反比例函數![]() 的圖像交于
的圖像交于![]() 、
、![]() 兩點,過點
兩點,過點![]() 作
作![]() 垂直
垂直![]() 軸于點
軸于點![]() ,連結
,連結![]() .若
.若![]() 的面積為2.
的面積為2.
(1)求![]() 的值;
的值;
(2)直接寫出:①點![]() 坐標____________;點
坐標____________;點![]() 坐標_____________;②當
坐標_____________;②當![]() 時,
時,![]() 的取值范圍__________________;
的取值范圍__________________;
(3)![]() 軸上是否存在一點
軸上是否存在一點![]() ,使
,使![]() 為直角三角形?若存在,求出點
為直角三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ,
,![]() ;②
;②![]() 或
或![]() ;(3)存在,
;(3)存在,![]() 坐標為
坐標為![]() 或
或![]() ,
,![]() 或
或![]() .
.
【解析】
(1)首先根據反比例函數與正比例函數的圖象特征,可知A、B兩點關于原點對稱,則O為線段AB的中點,故△BOC的面積等于△AOC的面積,都等于1,然后由反比例函數y=![]() 的比例系數k的幾何意義,可知△AOC的面積等于
的比例系數k的幾何意義,可知△AOC的面積等于![]() |k|,從而求出k的值;
|k|,從而求出k的值;
(2)聯立兩函數即可求出坐標,根據圖像可寫出范圍.
(3)設點![]() 坐標為
坐標為![]() 連結
連結![]() 、
、![]() ,再根據勾股定理解答即可.
,再根據勾股定理解答即可.
解:(1)由題意知:點![]() 與點
與點![]() 關于原點對稱,點
關于原點對稱,點![]() 為
為![]() 中點,
中點,
所以![]()
又 ![]()
所以![]()
所以![]()
![]()
(2)已知兩函數交于A,B兩點,
故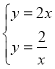
①點![]() 坐標
坐標![]() ,點
,點![]() 坐標
坐標![]()
②根據圖像可得即是反比例函數在正比例函數下方的范圍:![]() 或
或![]() .
.
(3)設點![]() 坐標為
坐標為![]() 連結
連結![]() 、
、![]() ;
;
∴![]()
或![]()
或![]()
當![]() 或
或![]() 或
或![]() 時,
時,
三角形![]() 為直角三角形,解得
為直角三角形,解得![]() 或
或![]() 或
或![]()
所以點![]() 坐標為
坐標為![]() 或
或![]() ,
,![]() 或
或![]()



 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,將一條數軸在原點O和點B處各折一下,得到一條“折線數軸”.圖中點A表示﹣11,點B表示10,點C表示18,我們稱點A和點C在數軸上相距29個長度單位.動點P從點A出發,以2單位/秒的速度沿著“折線數軸”的正方向運動,從點O運動到點B期間速度變為原來的一半,之后立刻恢復原速;同時,動點Q從點C出發,以1單位/秒的速度沿著數軸的負方向運動,從點B運動到點O期間速度變為原來的兩倍,之后也立刻恢復原速.設運動的時間為t秒.
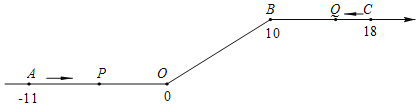
問:(1)動點P從點A運動至C點需要多少時間?
(2)P、Q兩點相遇時,求出相遇點M所對應的數是多少;
(3)求當t為何值時,P、O兩點在數軸上相距的長度與Q、B兩點在數軸上相距的長度相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】長為1,寬為a的矩形紙片(![]() ),如圖那樣折一下,剪下一個邊長等于矩形寬度的正方形(稱為第一次操作);再把剩下的矩形如圖那樣折一下,剪下一個邊長等于此時矩形寬度的正方形(稱為第二次操作);如此反復操作下去.若在第n此操作后,剩下的矩形為正方形,則操作終止.當n=3時,a的值為( )
),如圖那樣折一下,剪下一個邊長等于矩形寬度的正方形(稱為第一次操作);再把剩下的矩形如圖那樣折一下,剪下一個邊長等于此時矩形寬度的正方形(稱為第二次操作);如此反復操作下去.若在第n此操作后,剩下的矩形為正方形,則操作終止.當n=3時,a的值為( )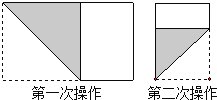
查看答案和解析>>
科目:初中數學 來源: 題型:
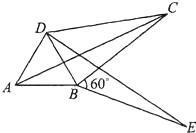
【題目】我們給出如下定義:若一個四邊形中存在相鄰兩邊的平方和等于一條對角線的平方,則稱這個四邊形為勾股四邊形,這兩條相鄰的邊稱為這個四邊形的勾股邊.
(1)寫出你所知道的四邊形中是勾股四邊形的兩種圖形的名稱_____,_____;
(2)如圖,將△ABC繞頂點B按順時針方向旋轉60°后得到△DBE,連接AD、DC,若∠DCB=30°,試證明;DC2+BC2=AC2.(即四邊形ABCD是勾股四邊形)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD對角線BD上截取BE=BC,連接CE并延長交AD于點F,連接AE,過B作BG⊥AE于點G,交AD于點H,則下列結論錯誤的是( )
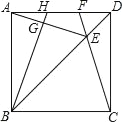
A. AH=DF B. S四邊形EFHG=S△DCF+S△AGH
C. ∠AEF=45° D. △ABH≌△DCF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了推動我區教育教學發展,加快教師的成長與提升,2018-2019學年度某名師工作室開展了多次送教下鄉活動.在某次研討課活動中,為了分析某節復習課的教學效果,課前,張老師讓八(![]() )班每位同學做
)班每位同學做![]() 道類似題目(與這節課內容相關)析某節復至少容對,解題情況如圖所示:課后,再讓學生做
道類似題目(與這節課內容相關)析某節復至少容對,解題情況如圖所示:課后,再讓學生做![]() 道類似的題目.結果如表所示.已知每位學生至少答對題.
道類似的題目.結果如表所示.已知每位學生至少答對題.
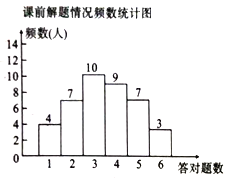
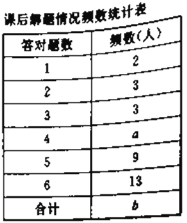
(1)根據圖表信息填空:![]() ;
;![]() .
.
(2)該班課前解題時答對題數的眾數是 ;課后答對題數的中位數是 .
(3)通過計算課前,課后學生答對題數的平均數,評價這節復習課的教學效果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明騎自行車上學,開始以正常速度勻速行駛,但行至中途自行車出了故障,只好停下來修車,車修后,因怕耽誤上課,他比修車前加快了騎車速度繼續勻速行駛,正面是行駛路程S(米)關于時間t(分)的函數圖象,那么符合這個同學行駛情況的圖象大致是( )
A.  B.
B. 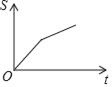
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(閱讀理解)小海喜歡研究數學問題,在計算整式加減(﹣4x2﹣7+5x)+(2x+3x2)的時候,想到了小學的列豎式加減法,令A=﹣4x2﹣7+5x,B=2x+3x2,然后將兩個整式關于x進行降冪排列,A=﹣4x2+5x﹣7,B=3x2+2x,最后只要寫出其各項系數對齊同類項進行豎式計算如下:
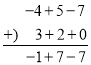
所以,(﹣4x2﹣7+5x)+(2x+3x2)=﹣x2+7x﹣7.
(模仿解題)若A=﹣4x2y2+2x3y﹣5xy3+2x4,B=3x3y+2x2y2﹣y4﹣4xy3,請你按照小海的方法,先對整式A,B關于某個字母進行降冪排列,再寫出其各項系數進行豎式計算A﹣B,并寫出A﹣B的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com