
【題目】已知三角形紙片![]() ,其中
,其中![]() ,
,![]() ,點
,點![]() 分別是
分別是![]() 上的點,連接
上的點,連接![]() .
.
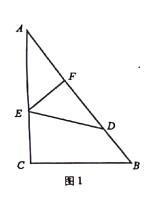
(1)如圖1,若將紙片![]() 沿
沿![]() 折疊,折疊后點
折疊,折疊后點![]() 剛好落在
剛好落在![]() 邊上點
邊上點![]() 處,且
處,且![]() ,求
,求![]() 的長;
的長;
(2)如圖2,若將紙片![]() 沿
沿![]() 折疊,折疊后點
折疊,折疊后點![]() 剛好落在
剛好落在![]() 邊上點
邊上點![]() 處,且
處,且![]() .
.
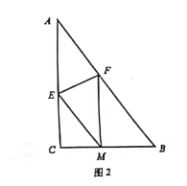
![]() 試判斷四邊形
試判斷四邊形![]() 的形狀,并說明理由;
的形狀,并說明理由;
![]() 求折痕
求折痕![]() 的長.
的長.
【答案】(1)![]() ;(2)
;(2)![]() 邊形
邊形![]() 是菱形,見解析,
是菱形,見解析,![]()
![]()
【解析】
(1)首先根據折疊的性質,得出AE=DE,AF=DF,然后根據等腰三角形三線合一的性質,得出∠AFE=90°,判定![]() ,再根據
,再根據![]() 得出
得出![]() 和
和![]() 的相似比為
的相似比為![]() ,即可得解;
,即可得解;
(2)①由折疊和平行的性質,得出![]() ,即可判定四邊形
,即可判定四邊形![]() 是菱形;
是菱形;
②首先過點![]() 作
作![]() 于點
于點![]() ,由
,由![]() 得出
得出![]() ,得出
,得出![]() ,然后根據
,然后根據![]() ,得出
,得出![]() ,進而得出FN、EN,根據勾股定理,即可求出EF.
,進而得出FN、EN,根據勾股定理,即可求出EF.
(1)根據題意,得AE=DE,AF=DF
∴根據等腰三角形三線合一的性質,得∠AFE=90°
又∵∠EAF=∠BAC,∠AEF=∠ABC
∴![]()
又∵![]() ,
,
∴![]() ,
,![]()
∴![]() 和
和![]() 的相似比為
的相似比為![]()
即![]()
又∵![]() ,
,![]() ,
,
∴![]()
(2)![]() 四邊形
四邊形![]() 是菱形
是菱形
由折疊的性質,得AE=EM,AF=FM,∠AEF=∠FEM,∠AFE=∠EFM
又∵![]()
∴∠FEM=∠AFE
∴∠AEF=∠AFE,∠FEM=∠EFM
∴![]() ,
,
∴四邊形![]() 是菱形
是菱形
![]() 過點
過點![]() 作
作![]() 于點
于點![]()

∵![]()
∴![]()
∴![]()
∵![]() ,
,![]() ,
,
∴![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]()
∴![]() ,
,
又∵![]()
∴![]()
∴


科目:初中數學 來源: 題型:
【題目】甲、乙兩個袋中均有三張除所標數值外完全相同的卡片,甲袋中的三張卡片上所標的數值分別為-7,-1,3,乙袋中的三張卡片上所標的數值分別為-2,1,6.先從甲袋中隨機取出一張卡片,用x表示取出的卡片上標的數值,再從乙袋中隨機取出一張卡片,用y表示取出的卡片上標的數值,把x、y分別作為點A的橫坐標、縱坐標.
(1)用適當的方法寫出點A(x,y)的所有情況;
(2)求點A落在第三象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若直線 y mx 8 和 y nx 3 都經過 x 軸上一點 B,與 y 軸分別交于 A 、C.

(1)寫出 A、C 兩點的坐標,A ,C ;
(2)若∠ABO=2∠CBO,求直線 AB 和 CB 的解析式;
(3)在(2)的條件下若另一條直線過點 B,且交 y 軸于 E,若△ABE 為等腰三角形,寫點 E 的坐標(只寫結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,連接
,連接![]() ,以對角線
,以對角線![]() 為邊按逆時針方向作矩形
為邊按逆時針方向作矩形![]() ,使矩形
,使矩形![]() 矩形
矩形![]() ;再連接
;再連接![]() ,以對角線
,以對角線![]() 為邊,按逆時針方向作矩形,使矩形
為邊,按逆時針方向作矩形,使矩形![]() 矩形
矩形![]() , ..按照此規律作下去,若矩形
, ..按照此規律作下去,若矩形![]() 的面積記作
的面積記作![]() ,矩形
,矩形![]() 的面積記作
的面積記作![]() ,矩形
,矩形![]() 的面積記作
的面積記作![]() , ... 則
, ... 則![]() 的值為__________.
的值為__________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著生活水平的不斷提高,越來越多的人選擇到電影院觀看電影,體驗視覺盛宴,并且更多的人通過網上平臺購票,既快捷又能享受更多優惠.某電影城2019年從網上購買![]() 張電影票的費用比現場購買
張電影票的費用比現場購買![]() 張電影票的費用少
張電影票的費用少![]() 元:從網上購買
元:從網上購買![]() 張電影票的費用和現場購買
張電影票的費用和現場購買![]() 張電影票的費用共
張電影票的費用共![]() 元.
元.
(1)求該電影城2019年在網上購票和現場購票每張電影票的價格為多少元?
(2)2019年五一當天,該電影城按照2019年網上購票和現場購票的價格銷售電影票,當天售出的總票數為![]() 張.五一假期過后,觀影人數出現下降,于是電影城決定從5月5日開始調整票價:現場購票價格下調,網上購票價格不變,結果發現,現場購票每張電影票的價格每降低
張.五一假期過后,觀影人數出現下降,于是電影城決定從5月5日開始調整票價:現場購票價格下調,網上購票價格不變,結果發現,現場購票每張電影票的價格每降低![]() 元,售出總票數就比五一當天增加
元,售出總票數就比五一當天增加![]() 張.經統計,5月5日售出的總票數中有
張.經統計,5月5日售出的總票數中有![]() 的電影票通過網上售出,其余通過現場售出,且當天票房總收入為
的電影票通過網上售出,其余通過現場售出,且當天票房總收入為![]() 元,試求出5月5日當天現場購票每張電影票的價格為多少元?
元,試求出5月5日當天現場購票每張電影票的價格為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正五邊形ABCDE中,連接AC、AD、CE,CE交AD于點F,連接BF,下列說法不正確的是()。

A. △CDH的周長等于AD+CD B. FC平分∠BFD C. AC2+BF2=4CD2 D. DE2=EF.CE
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,為美化校園環境,某校計劃在一塊長為60米,寬為40米的長方形空地上,修建一個長方形花圃,并將花圃四周余下的空地修建成同樣寬的甬道,設甬道的寬為a米.
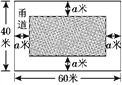 ①
①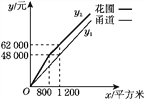 ②
②
(1)用含a的式子表示花圃的面積;
(2)如果甬道所占面積是整個長方形空地面積的![]() ,求此時甬道的寬;
,求此時甬道的寬;
(3)已知某園林公司修建甬道、花圃的造價y1(元)、y2(元)與修建面積x(平方米)之間的函數關系如圖②所示.如果學校決定由該公司承建此項目,并要求修建的甬道寬不少于2米且不超過10米,那么甬道的寬為多少米時,修建的甬道和花圃的總造價最低?最低總造價為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某加工廠為趕制一批零件,通過提高加工費標準的方式調動工人積極性.工人每天加工零件獲得的加工費y(元)與加工個數x(個)之間的部分函數圖象為折線OA-AB-BC,如圖所示.
(1)求工人一天加工零件不超過20個時每個零件的加工費.
(2)求40≤![]() ≤60時y與x的函數關系式.
≤60時y與x的函數關系式.
(3)小王兩天一共加工了60個零件,共得到加工費220元.在這兩天中,小王第一天加工零件不足20個,求小王第一天加工的零件個數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com