
【題目】如圖,AB是⊙O的直徑,AC是⊙O的切線,BC交⊙O于點E.
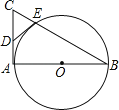
(1)若D為AC的中點,證明DE是⊙O的切線;
(2)若OA=![]() ,CE=1,求△ABC的面積.
,CE=1,求△ABC的面積.
【答案】(1)見解析;(2)2![]() .
.
【解析】
試題分析:(1)連接AE,OE,∠AEB=90°,∠BAC=90°,在Rt△ACE中,D為AC的中點,則DE=AD=CD=![]() AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,則∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出結論;
AC,得出∠DEA=∠DAE,由OA=OE,得出∠OAE=∠OEA,則∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,即可得出結論;
(2)AB=2AO=2![]() ,由△BCA∽△BAE,得出
,由△BCA∽△BAE,得出![]() =
=![]() ,求出BE=3,BC=4,由勾股定理得AC=
,求出BE=3,BC=4,由勾股定理得AC=![]() =2,則S△ABC=
=2,則S△ABC=![]() ABAC代入即可得出結果.
ABAC代入即可得出結果.
(1)證明:連接AE,OE,如圖所示:
∵AB是⊙O的直徑,
∴∠AEB=90°,
∵AC是⊙O的切線,
∴∠BAC=90°,
∵在Rt△ACE中,D為AC的中點,
∴DE=AD=CD=![]() AC,
AC,
∴∠DEA=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DEO=∠DEA+∠OEA=∠DAE+∠OAE=∠BAC=90°,
∴OE⊥DE,
∵OE為半徑,
∴DE是⊙O的切線;
(2)解:∵AO=![]() ,
,
∴AB=2AO=2![]() ,
,
∵∠CAB=∠AEB=90°,∠B=∠B,
∴△BCA∽△BAE,
∴![]() =
=![]() ,即AB2=BEBC=BE(BE+EC),
,即AB2=BEBC=BE(BE+EC),
∴(2![]() )2=BE2+BE,
)2=BE2+BE,
解得:BE=3或BE=﹣4(不合題意,舍去),
∴BE=3,
∴BC=BE+CE=3+1=4,
∴在Rt△ABC中,AC=![]() =
=![]() =2,
=2,
∴S△ABC=![]() ABAC=
ABAC=![]() ×2
×2![]() ×2=2
×2=2![]() .
.


科目:初中數學 來源: 題型:
【題目】(1)點A(3,-2)關于x軸的對稱點的坐標是 .
(2).若點(a,-2)與點(-3,b)關于x軸對稱,則a=__ __,b=__ __;若點(a,-2)與點(-3,b)關于y軸對稱,則a=__ __,b=__ __.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=x2﹣2x﹣3與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,該拋物線頂點為D,對稱軸交x軸于點H.
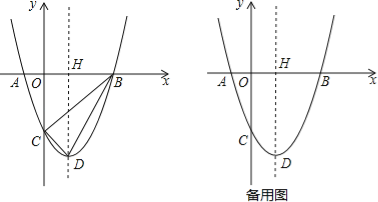
(1)求A,B兩點的坐標;
(2)設點P在x軸下方的拋物線上,當∠ABP=∠CDB時,求出點P的坐標;
(3)以OB為邊最第四象限內作等邊△OBM.設點E為x軸的正半軸上一動點(OE>OH),連接ME,把線段ME繞點M順時針旋轉60°得MF,求線段DF的長的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系xOy中,對于點P(a,b),若點P′的坐標為(a![]() ,ka+b)(其中k為常數,且k≠0),則稱點P′為點P的“k關聯點”.
,ka+b)(其中k為常數,且k≠0),則稱點P′為點P的“k關聯點”.
(1)求點P(﹣2,3)的“2關聯點”P′的坐標;
(2)若a、b為正整數,點P的“k關聯點”P′的坐標為(3,6),求出k及點P的坐標;
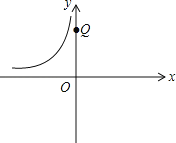
(3)如圖,點Q的坐標為(0,4![]() ),點A在函數y=﹣
),點A在函數y=﹣![]() (x<0)的圖象上運動,且點A是點B的“﹣
(x<0)的圖象上運動,且點A是點B的“﹣![]() 關聯點”,當線段BQ最短時,求B點坐標.
關聯點”,當線段BQ最短時,求B點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com