Question

【題目】已知,點P是Rt△ABC斜邊AB上一動點(不與A,B重合),分別過A,B向直線CP作垂線,垂足分別為E,F,Q為斜邊AB的中點.

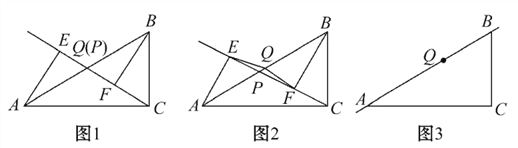
(1)如圖1,當點P與點Q重合時,AE與BF的位置關系是________,QE與QF的數量關系是________.

(2)如圖2,當點P在線段AB上不與點Q重合時,試判斷QE與QF的數量關系,并給予證明.

(3)如圖3,當點P在線段BA(或AB)的延長線上時,此時(2)中的結論是否成立?請畫出圖形并給予證明.

Answer 1

【答案】（1）AE∥BF，QE=QF；（2）QE=QF；（3）仍然成立

【解析】試題分析：（1）根據AAS推出△AEQ≌△BFQ，推出AE=BF即可；

（2）延長EQ交BF于D，求出△AEQ≌△BDQ，根據全等三角形的性質得出EQ=QD，根據直角三角形斜邊上中點性質得出即可；

（3）延長EQ交FB于D，求出△AEQ≌△BDQ，根據全等三角形的性質得出EQ=QD，根據直角三角形斜邊上中點性質得出即可．

試題解析：解：（1）如圖1，當點P與點Q重合時，AE與BF的位置關系是AE∥BF，QE與QF的數量關系是AE=BF，理由是：∵Q為AB的中點，∴AQ=BQ，∵AE⊥CQ，BF⊥CQ，∴AE∥BF，∠AEQ=∠BFQ=90°，在△AEQ和△BFQ中，∵∠AQE=∠BQF，∠AEQ=∠BFQ，AQ=BQ，∴△AEQ≌△BFQ，∴QE=QF，故答案為：AE∥BF，QE=QF；

（2）QE=QF，證明：如圖2，延長EQ交BF于D，∵由（1）知：AE∥BF，∴∠AEQ=∠BDQ，在△AEQ和△BDQ中，∵∠AQE=∠BQF，∠AEQ=∠BFQ，AQ=BQ，∴△AEQ≌△BDQ，∴EQ=DQ，∵∠BFE=90°，∴QE=QF；

（3）當點P在線段BA（或AB）的延長線上時，此時（2）中的結論成立．

證明：如圖3，延長EQ交FB于D，如圖3，

∵由（1）知：AE∥BF，∴∠AEQ=∠BDQ，在△AEQ和△BDQ中，∵∠AQE=∠BQF，∠AEQ=∠BFQ，AQ=BQ，

∴△AEQ≌△BDQ，∴EQ=DQ，∵∠BFE=90°，∴QE=QF．