
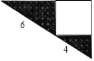
【題目】如圖所示是一個直角三角形的苗圃,由一個正方形花壇和兩塊直角三角形的草皮組成.如果兩個直角三角形的兩條斜邊長分別為4米和6米,則草皮的總面積為( )平方米.
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
【答案】C
【解析】
先根據相似三角形的判定定理得出△AMB∽△CBE,故可得出![]() =
=![]() 的值,設CE=x,則BC=2x,在Rt△CBE中根據勾股定理求出x的值,故可得出CE,AB=BC,AM=2AB的值,再根據S草皮=S△CBE+S△AMB,即可得出結論.
的值,設CE=x,則BC=2x,在Rt△CBE中根據勾股定理求出x的值,故可得出CE,AB=BC,AM=2AB的值,再根據S草皮=S△CBE+S△AMB,即可得出結論.
解:∵△MDE是直角三角形,四邊形ABCD是正方形,
∴∠MAB=∠BCE=90°,∠M+∠ABM=90°,∠ABM+∠CBE=90°,
∴∠M=∠CBE,
∴△AMB∽△CBE,
∴![]() =
=![]() ,
,
∵MB=6,BE=4,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∵AB=BC,
∴![]() =
=![]() ,
,
設CE=2x,則BC=3x,在Rt△CBE中,BE2=BC2+CE2,即42=(3x)2+(2x)2,解得x=![]() ,
,
∴CE=![]() ,AB=BC=
,AB=BC=![]() ,AM=
,AM=![]() AB=
AB=![]() ,
,
∴S草皮=S△CBE+S△AMB=![]() ×
×![]() ×
×![]() +
+![]() ×
×![]() ×
×![]() =12.
=12.
故選:C.


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:初中數學 來源: 題型:
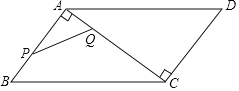
【題目】如圖,在ABCD中,AB=6,BC=10,AB⊥AC,點P從點B出發沿著B→A→C的路徑運動,同時點Q從點A出發沿著A→C→D的路徑以相同的速度運動,當點P到達點C時,點Q隨之停止運動,設點P運動的路程為x,y=PQ2,下列圖象中大致反映y與x之間的函數關系的是( )
A. 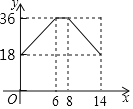 B.
B. 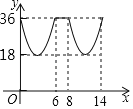
C. 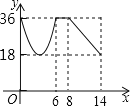 D.
D. 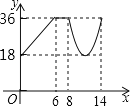
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,D是等邊三角形ABC內一點,將線段AD繞點A順時針旋轉60°,得到線段AE,連接CD,BE.
(1)求證:∠AEB=∠ADC;
(2)連接DE,若∠ADC=105°,求∠BED的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進一種每件價格為90元的新商品,在商場試銷時發現:銷售單價![]() 元
元![]() 件
件![]() 與每天銷售量
與每天銷售量![]() 件
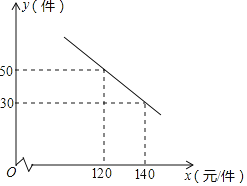
件![]() 之間滿足如圖所示的關系.
之間滿足如圖所示的關系.
![]() 求出y與x之間的函數關系式;
求出y與x之間的函數關系式;
![]() 寫出每天的利潤W與銷售單價x之間的函數關系式,并求出售價定為多少時,每天獲得的利潤最大?最大利潤是多少?
寫出每天的利潤W與銷售單價x之間的函數關系式,并求出售價定為多少時,每天獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
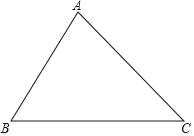
【題目】如圖,在某海上觀測點B處觀測到位于北偏東30°方向有一艘救船A,搜救船A最大航速50海里/時,AB=52![]() 海里,在位于觀測點B的正東方向,搜救船A的東南方向有一失事漁船C,由于當天正值東南風,失事漁船C以2海里/時的速度向西北方向漂移,若不考慮大風對搜救船A的航線和航速的影響,求失事漁船獲救的最快時間.
海里,在位于觀測點B的正東方向,搜救船A的東南方向有一失事漁船C,由于當天正值東南風,失事漁船C以2海里/時的速度向西北方向漂移,若不考慮大風對搜救船A的航線和航速的影響,求失事漁船獲救的最快時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A、B、C三人玩籃球傳球游戲,游戲規則是:第一次傳球由A將球隨機地傳給B,C兩人中的某一人,以后的每一次傳球都是由上次的傳球者隨機地傳給其他兩人中的某一人.
(1)求兩次傳球后,球恰在B手中的概率;
(2)求三次傳球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC是一塊直角三角板,且∠C=90°,∠A=30°,現將圓心為點O的圓形紙片放置在三角板內部,將圓形紙片沿著三角板的內部邊緣滾動1周,回到起點位置時停止,若BC=7+2![]() ,圓形紙片的半徑為2,求圓心O運動的路徑長為_____.
,圓形紙片的半徑為2,求圓心O運動的路徑長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
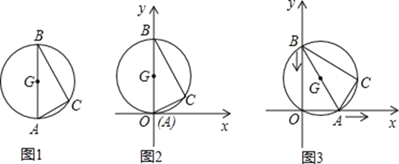
【題目】圖1是用鋼絲制作的一個幾何探究工具,其中△ABC內接于⊙G,AB是⊙G的直徑,AB=6,AC=2.現將制作的幾何探究工具放在平面直角坐標系中(如圖2),然后點A在射線OX上由點O開始向右滑動,點B在射線OY上也隨之向點O滑動(如圖3),當點B滑動至與點O重合時運動結束. 在整個運動過程中,點C運動的路程是( )
A. 4 B. 6 C. 4![]() ﹣2 D. 10﹣4
﹣2 D. 10﹣4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=9x2﹣6ax+a2﹣b
(1)當b=﹣3時,二次函數的圖象經過點(﹣1,4)
①求a的值;
②求當a≤x≤b時,一次函數y=ax+b的最大值及最小值;
(2)若a≥3,b﹣1=2a,函數y=9x2﹣6ax+a2﹣b在﹣![]() <x<c時的值恒大于或等于0,求實數c的取值范圍.
<x<c時的值恒大于或等于0,求實數c的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com