
【題目】定義:如果兩條線段將一個三角形分成 3個等腰三角形,我們把這兩條線段叫做這個三角形的“三分線”.例如:如圖①,線段![]() 、
、![]() 把一個頂角為
把一個頂角為![]() 的等腰
的等腰![]() 分成了 3個等腰三角形,則線段
分成了 3個等腰三角形,則線段![]() 、
、![]() 就是等腰
就是等腰![]() 的“三分線”.
的“三分線”.

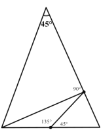
(1)圖②是一個頂角為 45°的等腰三角形,在圖中畫出“三分線”,并標出每個等腰三角形頂角的度數.
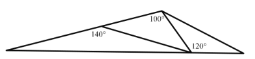
(2)如圖③,在![]() 邊上取一點
邊上取一點![]() ,令
,令![]() 可以分割出第一個等腰
可以分割出第一個等腰![]() ,接著又需要考慮如何將
,接著又需要考慮如何將![]() 分成2個等腰三角形,即可畫出所需要的“三分線”,類比該方法,在圖④中畫出
分成2個等腰三角形,即可畫出所需要的“三分線”,類比該方法,在圖④中畫出![]() 的“三分線”,并標出每個等腰三角形頂角的度數;
的“三分線”,并標出每個等腰三角形頂角的度數;

(3)在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
①畫出![]() ;(尺規畫圖,不寫作法,保留作圖痕跡)
;(尺規畫圖,不寫作法,保留作圖痕跡)
②畫出![]() 的“三分線”,并做適當的標注.
的“三分線”,并做適當的標注.

【答案】(1)見解析;(2)見解析;(3)①見解析;②見解析
【解析】
(1)根據“三分線”的定義,可以分成的三個等腰三角形三個內角度數分別為:45°、45°、90°;22.5°、22.5°、135°;67.5°、67.5°、45°;
(2)根據“三分線”的定義,可以分成的三個等腰三角形三個內角度數分別為:20°、20°、140°;40°、40°、100°;30°、30°、120°;
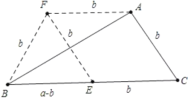
(3)①以a-b、b、b為邊作△BEF,,再作邊長為b的菱形EFAC(FA∥BE),即可得出△ABC;
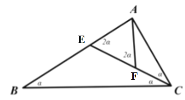
②根據“三分線”的定義,圖中△BCE、△AEF、△AFC都是等腰三角形,則線段CE、AF就是“三分線”.
解:(1)如下圖,
(2)如下圖
(3)①作法:以a-b、b、b為邊作△BEF,再作邊長為b的菱形EFAC(FA∥BE),如圖所示,
②如下圖,


 期末100分闖關海淀考王系列答案
期末100分闖關海淀考王系列答案 小學能力測試卷系列答案
小學能力測試卷系列答案科目:初中數學 來源: 題型:
【題目】城市中“打車難”一直是人們關注的一個社會熱點問題.近幾年來,“互聯網+”戰略與傳統出租車行業深度融合,“優步”、“滴滴出行”等打車軟件就是其中典型的應用,名為“數據包絡分析”(簡稱DEA)的一種效率評價方法,可以很好地優化出租車資源配置,為了解出租車資源的“供需匹配”,北京、上海等城市對每天24個時段的DEA值進行調查,調查發現,DEA值越大,說明匹配度越好.在某一段時間內,北京的DEA值y與時刻t的關系近似滿足函數關系![]() (a,b,c是常數,且
(a,b,c是常數,且![]() ≠0),如圖記錄了3個時刻的數據,根據函數模型和所給數據,當“供需匹配”程度最好時,最接近的時刻t是( )
≠0),如圖記錄了3個時刻的數據,根據函數模型和所給數據,當“供需匹配”程度最好時,最接近的時刻t是( )

A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,已知AB=AC,∠BAC=90°,D是BC上一點,EC⊥BC,CE=BD
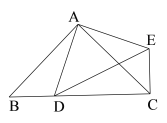
求證:(1)△ABD≌△ACE;(2)試判斷△ADE的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,平面直角坐標的原點是等邊三角形的中心,A(0,1),把△ABC繞點 O 順時針旋轉,每秒旋轉 60°,則第 2018 秒時,點 A 的坐標為( )

A. (0,1) B. (﹣![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=2,∠B=∠C=40°,點D在線段BC上運動(D不與B、C重合),連接AD,作∠ADE=40°,DE交線段AC于E.
(1)當∠BDA=115°時,∠EDC= °,∠DEC= °;點D從B向C運動時,∠BDA逐漸變 (填“大”或“小”);
(2)當DC等于多少時,△ABD≌△DCE,請說明理由;
(3)在點D的運動過程中,△ADE的形狀可以是等腰三角形嗎?若可以,請直接寫出∠BDA的度數.若不可以,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=a(x+1)2 (a≠0)的圖象經過點A(1,8).
(1)求此二次函數的表達式;
(2)寫出這個二次函數圖象的頂點坐標、對稱軸;
(3)試判斷點B(-2,2)和C(m,2m-1)是否在此二次函數的圖象上?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:對于給定的兩個函數,任取自變量x的一個值,當x<0時,它們對應的函數值互為相反數;當x≥0時,它們對應的函數值相等,我們稱這樣的兩個函數互為相關函數.例如:一次函數y=x﹣1,它們的相關函數為![]() .
.
(1)已知點A(﹣3,6)在一次函數y=ax﹣3的相關函數的圖象上,求a的值;
(2)已知二次函數y=-2x2+3.
①當點B(m,3)在這個函數的相關函數的圖象上時,求m的值;
②當﹣2≤x≤2時,求函數y=-2x2+3的相關函數的最大值和最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點O為坐標原點,直線y=﹣x+b與坐標軸交于C,D兩點,直線AB與坐標軸交于A,B兩點,線段OA,OC的長是方程x2﹣3x+2=0的兩個根(OA>OC).
(1)求點A,C的坐標;
(2)直線AB與直線CD交于點E,若點E是線段AB的中點,反比例函數y=![]() (k≠0)的圖象的一個分支經過點E,求k的值;
(k≠0)的圖象的一個分支經過點E,求k的值;
(3)在(2)的條件下,點M在直線CD上,坐標平面內是否存在點N,使以點B,E,M,N為頂點的四邊形是菱形?若存在,請直接寫出滿足條件的點N的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CD⊥AB于點D,點E在CD上,下列四個條件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,將其中兩個作為條件,不能判定△ADC≌△EDB的是
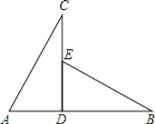
A.①②B.①④C.②③D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com