
【題目】如圖,矩形紙片![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 上一動點,
上一動點,![]() 沿
沿![]() 折疊,點
折疊,點![]() 落在點
落在點![]() 處;延長
處;延長![]() 交
交![]() 于
于![]() 點,連接
點,連接![]() .
.
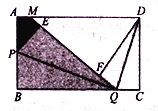
(1)求證:![]() ≌
≌![]() ;
;
(2)當![]() 時,將
時,將![]() 沿
沿![]() 折疊,點
折疊,點![]() 落在線段
落在線段![]() 上點
上點![]() 處.
處.
①求證:![]() ∽
∽![]() ;
;
②如果![]() ,
,![]() ,求
,求![]() 的長.
的長.
【答案】(1)見解析;(2)①見解析;②6
【解析】
(1)依據“HL”進行證明即可;
(2)①由矩形的性質得AD∥BC,可得∠AME=∠CQF,然后由全等三角形的性質和折疊的性質得出![]() ,∠DQC=∠DQF,即可得到∠AMP=∠DQC,再由
,∠DQC=∠DQF,即可得到∠AMP=∠DQC,再由![]() ,即可證得
,即可證得![]() ∽
∽![]() ;
;
②設![]() ,證得
,證得![]() ∽
∽![]() ,依據相似三角形的對應邊成比例可得
,依據相似三角形的對應邊成比例可得![]() ,由
,由![]() ∽
∽![]() 得
得![]() ,可得
,可得![]() ,AM=x2+1,由折疊性質得DF=2x,然后在Rt△FDM中利用三角函數列出方程即可求出x的值,即可得到本題的答案.
,AM=x2+1,由折疊性質得DF=2x,然后在Rt△FDM中利用三角函數列出方程即可求出x的值,即可得到本題的答案.
解:(1)∵四邊形![]() 是矩形
是矩形
∴![]()
根據折疊的性質可知:![]() ,
,![]()
∵![]() 點為
點為![]() 中點
中點
∴![]()
又∵![]()
∴![]() ≌
≌![]()
(2)①∵四邊形![]() 是矩形,
是矩形,
∴AD∥BC,
∴∠AME=∠CQF,
由(1)知![]() ≌
≌![]() ,
,
∴![]() ,
,
∵將![]() 沿
沿![]() 折疊,點
折疊,點![]() 落在線段
落在線段![]() 上點
上點![]() 處,
處,
∴∠DQC=∠DQF,
∴∠AMP=∠DQC,
又∵![]() ,
,
∴![]() ∽
∽![]() ;
;
②設![]() ,則
,則![]() ,
,![]()
由(1)知![]() ≌
≌![]()
∴![]()
根據折疊的性質可知:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]()
由![]() ∽
∽![]() 得,
得,![]() ,即
,即![]() ,
,
![]() ,
,
又∵在![]() 中,
中,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,整理得,
,整理得,![]() ,
,
解方程得:![]() ,
,![]() (不合題意,舍去).
(不合題意,舍去).
∴![]() .
.


 贏在課堂名師課時計劃系列答案
贏在課堂名師課時計劃系列答案 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案科目:初中數學 來源: 題型:
【題目】學校運動會的立定跳遠和1分鐘跳繩兩個單項比賽分成預賽和決賽兩個階段.下表為參加這兩項比賽的10名學生的預賽成績:
學生編號 成績 項目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳遠(單位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分鐘跳繩(單位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在這10名學生中,同時進入兩項決賽的只有6人,進入立定跳遠決賽的有8![]() 的值是__________.
的值是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如我們把函數![]() 沿
沿![]() 軸翻折得到函數
軸翻折得到函數![]() ,函數
,函數![]() 與函數
與函數![]() 的圖象合起來組成函數
的圖象合起來組成函數![]() 的圖象.若直線
的圖象.若直線![]() 與函數
與函數![]() 的圖象剛好有兩個交點,則滿足條件的
的圖象剛好有兩個交點,則滿足條件的![]() 的值可以為_______________(填出一個合理的值即可).
的值可以為_______________(填出一個合理的值即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
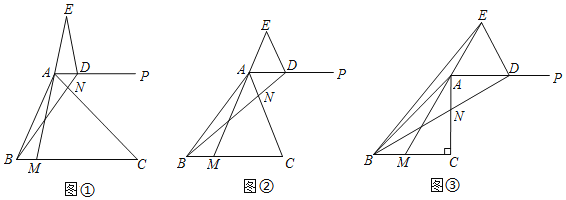
【題目】在△ABC中,CA=CB,0°<∠C≤90°.過點A作射線AP∥BC,點M、N分別在邊BC、AC上(點M、N不與所在線段端點重合),且BM=AN,連結BN并延長交AP于點D,連結MA并延長交AD的垂直平分線于點E,連結ED.
(猜想)如圖①,當∠C=45°時,可證△BCN≌△ACM,從而得出∠CBN=∠CAM,進而得出∠BDE的大小為 度.
(探究)如圖②,若∠C=α.
(1)求證:△BCN≌△ACM.
(2)∠BDE的大小為 度(用含a的代數式表示).
(應用)如圖③,當∠C=90°時,連結BE.若BC=3,∠BAM=15°,則△BDE的面積為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,點D,E分別是邊AB,AC上的點,DE∥BC,點H是邊BC上的點,連接AH交線段DE于點G,且BH=DE=12,DG=8,S△ADG=12,則S四邊形BCED=( )

A.24B.22.5C.20D.25
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖![]() ,
,![]() ,
,![]() ,
,![]() .點
.點![]() 從
從![]() 開始沿邊
開始沿邊![]() 向點
向點![]() 以
以![]() 的速度移動,與此同時,點
的速度移動,與此同時,點![]() 從點
從點![]() 開始沿邊
開始沿邊![]() 向點
向點![]() 以
以![]() 的速度移動.如果
的速度移動.如果![]() 、
、![]() 分別從
分別從![]() 、
、![]() 同時出發,當點
同時出發,當點![]() 運動到點
運動到點![]() 時,兩點停止運動,問:
時,兩點停止運動,問:
![]() 經過幾秒,
經過幾秒,![]() 的面積等于
的面積等于![]() ?
?
(2)![]() 的面積會等于
的面積會等于![]() 嗎?若會,請求出此時的運動時間;若不會,請說明理由.
嗎?若會,請求出此時的運動時間;若不會,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com