【題目】閱讀下列材料，并回答問題.事實上，在任何一個直角三角形中，兩條直角邊的平方之和一定等于斜邊的平方，這個結論就是著名的勾股定理.請利用這個結論，完成下面活動:
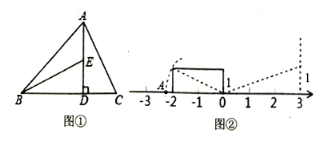
一個直角三角形的兩條直角邊分別為
，那么這個直角三角形斜邊長為____；
如圖①，
于
，求
的長度；
如圖②，點
在數軸上表示的數是____請用類似的方法在圖2數軸上畫出表示數
的
點(保留痕跡).
黃岡小狀元同步計算天天練系列答案科目：初中數學 來源： 題型：
【題目】如圖，已知△ABC中，∠ABC=90°．
（1）尺規作圖：按下列要求完成作圖（保留作圖痕跡，請標明字母）
①作線段AC的垂直平分線l，交AC于點O；
②連接BO并延長，在BO的延長線上截取OD，使得OD=OB；
③連接DA、DC．
（2）判斷四邊形ABCD的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知二次函數圖象的頂點在原點
，對稱軸為
軸．一次函數
的圖象與二次函數的圖象交于
，
兩點（在的左側），且點坐標為
．平行于
軸的直線
過
點．
求一次函數與二次函數的解析式；
判斷以線段
為直徑的圓與直線的位置關系，并給出證明；
把二次函數的圖象向右平移
個單位，再向下平移
個單位
，二次函數的圖象與軸交于
，
兩點，一次函數圖象交軸于
點．當為何值時，過，，三點的圓的面積最小？最小面積是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
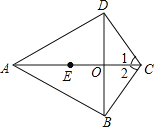
【題目】如圖，在四邊形ABCD中，AB=AD，BC=DC，AC、BD相交于點O，點E在AO上，且OE=OC.
（1）求證：∠1=∠2；
（2）連結BE、DE，判斷四邊形BCDE的形狀，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知直線AB：y=kx+b經過點B（1，4）、A（5，0）兩點，且與直線y=2x-4交于點C．
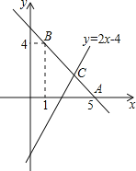
（1）求直線AB的解析式并求出點C的坐標；
（2）求出直線y=kx+b、直線y=2x-4及與y軸所圍成的三角形面積；
（3）現有一點P在直線AB上，過點P作PQ∥y軸交直線y=2x-4于點Q，若線段PQ的長為3，求點P的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（材料閱讀）我們曾解決過課本中的這樣一道題目：
如圖，四邊形
是正方形，
為
邊上一點，延長
至
，使
，連接
.……
提煉1：
繞點
順時針旋轉90°得到
；
提煉2：
；
提煉3：旋轉、平移、軸對稱是圖形全等變換的三種方式.
（問題解決）（1）如圖，四邊形是正方形，為邊上一點，連接
，將
沿折疊，點
落在
處，
交
于點，連接
.可得：
°；
三者間的數量關系是
（2）如圖，四邊形的面積為8，
，
，連接
.求的長度.
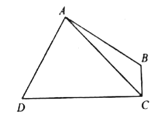
（3）如圖，在
中，
，
，點
在邊上，
.寫出
間的數量關系，并證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，直線
與
軸交于點
，與
軸交于點
，與直線
相交于點
，
（1）求直線
的函數表達式；
（2）求
的面積；
（3）在 軸上是否存在一點
，使
是等腰三角形．若不存在，請說明理由；若存在，請直接寫出點 的坐標
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，等腰三角形ABC底邊BC的長為4 cm，面積為12 cm2，腰AB的垂直平分線EF交AB于點E，交AC于點F，若D為BC邊上的中點，M為線段EF上一點，則△BDM的周長最小值為( )
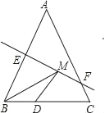
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
