
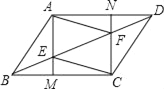
【題目】如圖,已知平行四邊形ABCD,過A點作AM⊥BC于M,交BD于E,過C點作CN⊥AD于N,交BD于F,連接AF、CE.
(1)求證:四邊形AECF為平行四邊形;
(2)當AECF為菱形,M點為BC的中點時,求AB:AE的值.
【答案】(1)證明見解析;(2)AB:AE=![]() :1.
:1.
【解析】(1)證明∵四邊形ABCD是平行四邊形(已知),
∴BC∥AD(平行四邊形的對邊相互平行)。
又∵AM丄BC(已知),∴AM⊥AD。
∵CN丄AD(已知),∴AM∥CN。∴AE∥CF。
又由平行得∠ADE=∠CBD,又AD=BC(平行四邊形的對邊相等)。
在△ADE和△CBF中, ∠DAE=∠BCF="90" ,AD=CB,∠ADE=∠FBC,
∴△ADE≌△CBF(ASA),∴AE=CF(全等三角形的對應邊相等)。
∴四邊形AECF為平行四邊形(對邊平行且相等的四邊形是平行四邊形)。
(2)如圖,連接AC交BF于點0,當AECF為菱形時,則AC與EF互相垂直平分。
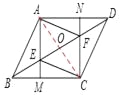
∵BO=OD(平行四邊形的對角線相互平分),
∴AC與BD互相垂直平分。
∴![]() ABCD是菱形(對角線相互垂直平分的平行四邊形是菱形)。
ABCD是菱形(對角線相互垂直平分的平行四邊形是菱形)。
∴AB=BC(菱形的鄰邊相等)。
∵M是BC的中點,AM丄BC(已知),∴△ABM≌△CAM。
∴AB=AC(全等三角形的對應邊相等)。∴△ABC為等邊三角形。
∴∠ABC=60°,∠CBD=30°。
在Rt△BCF中,CF:BC=tan∠CBF=![]() 。
。
又∵AE=CF,AB=BC,∴AB:AE=![]() 。
。
(1)根據平行四邊形的性質、垂直的定義、平行線的判定定理可以推知AE∥CF;然后由ASA推知△ADE≌△CBF;最后根據全等三角形的對應邊相等知AE=CF,根據對邊平行且相等的四邊形是平行四邊形的判定得出結論。
(2)如圖,連接AC交BF于點0.由菱形的判定定理推知平行四邊形ABCD是菱形,根據菱形的鄰邊相等知AB=BC;然后結合已知條件“M是BC的中點,AM丄BC”證得△ADE≌△CBF(ASA),所以AE=CF(全等三角形的對應邊相等),從而證得△ABC是正三角形;最后在Rt△BCF中,利用銳角三角函數的定義求得CF:BC=tan∠CBF=![]() ,利用等量代換知(AE=CF,AB=BC)AB:AE=
,利用等量代換知(AE=CF,AB=BC)AB:AE=![]() 。
。


 小學期末標準試卷系列答案
小學期末標準試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,四邊形ABCD是矩形,AD∥x軸,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.

(1)直接寫出B、C、D三點的坐標;
(2)將矩形ABCD向右平移m個單位,使點A、C恰好同時落在反比例函數![]() (
(![]() )的圖象上,得矩形A′B′C′D′.求矩形ABCD的平移距離m和反比例函數的解析式.
)的圖象上,得矩形A′B′C′D′.求矩形ABCD的平移距離m和反比例函數的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=![]() x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.
x+4與x軸、y軸分別交于點A和點B,點C,D分別為線段AB,OB的中點,點P為OA上一動點,PC+PD值最小時點P的坐標為.

A. (-3,0) B. (-6,0) C. (-![]() ,0) D. (-
,0) D. (-![]() ,0)
,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是正方形,點P,Q分別在邊AB,BC的延長線上且BP=CQ,連接AQ,DP交于點O,并分別與邊CD,BC交于點F,E,連接AE,下列結論:①AQ⊥DP;②△OAE∽△OPA;③當正方形的邊長為3,BP=1時,cos∠DFO=![]() ,其中正確結論的個數是( )
,其中正確結論的個數是( )
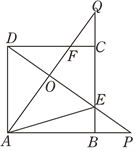
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,對于點Pa,b和點Qa,b,給出如下定義:若![]() ,則稱點Q為點P的限變點,例如:點(2,3)的限變點的坐標是(2,3),點2,5的限變點的坐標是2,5。
,則稱點Q為點P的限變點,例如:點(2,3)的限變點的坐標是(2,3),點2,5的限變點的坐標是2,5。
(1)在點A2,1,B1,2中有一個點是函數y=![]() 圖象上某一個點的限變點,這個點是 ;
圖象上某一個點的限變點,這個點是 ;
(2)求點![]() ,1的限變點的坐標;
,1的限變點的坐標;
(3)若點P在函數yx32xk,k2的圖象上,其限變點Q的縱坐標b的取值范圍是5b2,求k的取值范圍。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某射擊隊教練為了了解隊員訓練情況,從隊員中選取甲、乙兩名隊員進行射擊測試,相同條件下各射靶5次,成績統計如下:

(1)根據上述信息可知:甲命中環數的中位數是 環,乙命中環數的眾數是 環;
(2)試通過計算說明甲、乙兩人的成績誰比較穩定?
(3)如果乙再射擊1次,命中8環,那么乙射擊成績的方差會 .(填 “變大”、“變小” 或 “不變”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個工程隊都參與某筑路工程,先由甲隊筑路60千米,再由乙隊完成剩下的筑路工程,已知乙隊筑路總千米數是甲隊筑路總千米數的![]() 倍,甲隊比乙隊多筑路20天.如果甲、乙兩隊平均每天筑路千米數之比為5∶8,求乙隊平均每天筑路多少千米?
倍,甲隊比乙隊多筑路20天.如果甲、乙兩隊平均每天筑路千米數之比為5∶8,求乙隊平均每天筑路多少千米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前節能燈在城市已基本普及,今年山東省面向縣級及農村地區推廣,為響應號召,某商場計劃購進甲,乙兩種節能燈共![]() 只,這兩種節能燈的進價、售價如下表:
只,這兩種節能燈的進價、售價如下表:
進價(元/只) | 售價(元/只) | |
甲型 |
|
|
乙型 |
|
|
(1)如何進貨,進貨款恰好為![]() 元?
元?
(2)設商場購進甲種節能燈![]() 只,求出商場銷售完節能燈時總利潤
只,求出商場銷售完節能燈時總利潤![]() 與購進甲種節能燈
與購進甲種節能燈![]() 之間的函數關系式;
之間的函數關系式;
(3)如何進貨,商場銷售完節能燈時獲利最多且不超過進貨價的![]() ,此時利潤為多少元?
,此時利潤為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com