
【題目】如圖,四邊形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
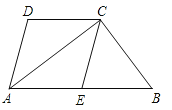
(1)求證:四邊形AECD是菱形;
(2)若點E是AB的中點,試判斷△ABC的形狀,并說明理由.
【答案】證明:
(1)∵AB∥CD,即AE∥CD,
又∵CE∥AD,∴四邊形AECD是平行四邊形. 2分
∵AC平分∠BAD,∴∠CAE=∠CAD,
又∵AD∥CE,∴∠ACE=∠CAD,
∴∠ACE=∠CAE,
∴AE=CE,
∴四邊形AECD是菱形;········· 4分
(2)證法一:∵E是AB中點,∴AE=BE.
又∵AE=CE,∴BE=CE,∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180°,
∴2∠BCE+2∠ACE=180°,∴∠BCE+∠ACE=90°.
即∠ACB=90°,∴△ABC是直角三角形.
證法二:連DE,則DE⊥AC,且平分AC,
設DE交AC于F,∵E是AB的中點,∴EF∥BC.
∴BC⊥AC,∴△ABC是直角三角形.······· 8分
【解析】
試題(1)先根據平行四邊形的定義證得四邊形AECD是平行四邊形,根據平行線的性質可得∠ACE=∠CAD,再結合角平分線的性質可得AE=CE,從而證得結論;(2)由AE=CE,AE=BE可得BE=CE,即可得到∠B=∠BCE,由∠B+∠BCA+∠BAC=180可得2∠BCE+2∠ACE=180,即可得到結果.
(1)∵AB∥CD, CE∥AD,
∴四邊形AECD是平行四邊形.
∵CE∥AD,
∴∠ACE=∠CAD.
∵AC平分∠BAD,
∴∠CAE=∠CAD.
∴∠ACE=∠CAE,
∴AE=CE.
∴四邊形AECD是菱形;
(2)∵AE=CE,AE=BE,
∴BE=CE,
∴∠B=∠BCE,
∵∠B+∠BCA+∠BAC=180,
∴2∠BCE+2∠ACE=180,
∴∠BCE+∠ACE=90,即∠ACB=90.
∴△ABC是直角三角形.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在△OAB中,∠OAB=90,∠AOB=30,OB=8.以OB為一邊,在△OAB外作等邊三角形OBC,D是OB的中點,連接AD并延長交OC于E.
【1】求點B的坐標
【2】求證:四邊形ABCE是平行四邊形;
【3】如圖2,將圖1中的四邊形ABCO折疊,使點C與點A重合,折痕為FG,求OG的長.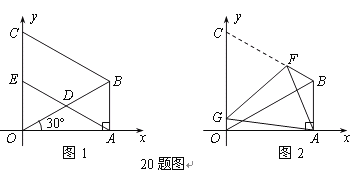
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點P是正方形ABCD內一點,點P到點A,B和C的距離分別為![]() ,1,2
,1,2![]() ,△ABP繞點B旋轉至△CBP′,連結PP′,并延長BP與DC相交于點Q,則∠CPQ的大小為______ (度)
,△ABP繞點B旋轉至△CBP′,連結PP′,并延長BP與DC相交于點Q,則∠CPQ的大小為______ (度)
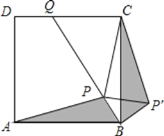
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線![]() ,直線
,直線![]() 交
交![]() 于
于![]() 點,交
點,交![]() 于
于![]() 點,
點,![]() 是線段
是線段![]() 上的一個動點,
上的一個動點,
(1)若![]() 點在線段
點在線段![]() (
(![]() 、
、![]() 兩點除外)上運動,問
兩點除外)上運動,問![]() ,
,![]() ,
,![]() 之間的關系是什么?這種關系是否變化?
之間的關系是什么?這種關系是否變化?
(2)若![]() 點在線段
點在線段![]() 之外時,
之外時,![]() ,
,![]() ,
,![]() 之間的關系怎樣?說明理由
之間的關系怎樣?說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
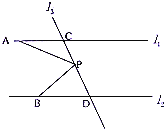
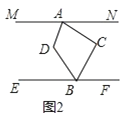
【題目】如圖,已知直線![]() .
.![]() 這兩直線之間一點.
這兩直線之間一點.
(1)如圖1,若![]() 與
與![]() 的平分線相交于點
的平分線相交于點![]() ,若
,若![]() ,求
,求![]() 的度數.
的度數.

(2)如圖2,若![]() 與
與![]() 的平分線相交于點
的平分線相交于點![]() ,
,![]() 與
與![]() 有何數量關系?并證明你的結論.
有何數量關系?并證明你的結論.
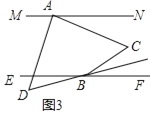
(3)如圖3,若![]() 的平分線與
的平分線與![]() 的平分線所在的直線相交于點
的平分線所在的直線相交于點![]() ,請直接寫出
,請直接寫出![]() 與
與![]() 之間的數量關系.
之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
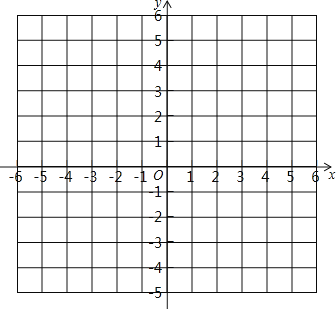
【題目】已知在平面直角坐標系中有三點![]() 、
、![]() 、
、![]() ,請回答如下問題:
,請回答如下問題:
(1)在坐標系內描出點![]() 的位置:
的位置:
(2)求出以![]() 三點為頂點的三角形的面積;
三點為頂點的三角形的面積;
(3)在![]() 軸上是否存在點
軸上是否存在點![]() ,使以
,使以![]() 三點為頂點的三角形的面積為10,若存在,請直接寫出點
三點為頂點的三角形的面積為10,若存在,請直接寫出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王大伯幾年前承包了甲、乙兩片荒山,各栽100棵楊梅樹,成活98%.現已掛果,經濟效益初步顯現,為了分析收成情況,他分別從兩山上隨意各采摘了4棵樹上的楊梅,每棵的產量如折線統計圖所示.
(1)分別計算甲、乙兩山樣本的平均數,并估算出甲、乙兩山楊梅的產量總和;
(2)試通過計算說明,哪個山上的楊梅產量較穩定?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=ax+b(a≠0)的圖象與反比例函數y= ![]() 的圖象相交于A、B兩點,以AB為邊,在直線AB的左側作菱形ABCD,邊BC⊥y軸于點E,若點A坐標為(m,6),tan∠BOE=
的圖象相交于A、B兩點,以AB為邊,在直線AB的左側作菱形ABCD,邊BC⊥y軸于點E,若點A坐標為(m,6),tan∠BOE= ![]() ,OE=
,OE= ![]() .
.
(1)求反比例函數和一次函數的解析式;
(2)求點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農業觀光園將一塊面積為![]() 的觀光園分成
的觀光園分成![]() 三個區域,分別種植甲、乙、丙三種花卉,且每平方米栽種甲
三個區域,分別種植甲、乙、丙三種花卉,且每平方米栽種甲![]() 株或乙
株或乙![]() 株或丙
株或丙![]() 株.已知
株.已知![]() 區域的面積是
區域的面積是![]() 的
的![]() 倍,記A區域的面積為
倍,記A區域的面積為![]() 區域的面積為
區域的面積為![]() .
.
花卉 項目 | 甲 | 乙 | 丙 |
面積 |
|
| |
株/ |
|
|
|
數量 |
|
(1)完成上表(結果用含![]() 的代數式表示).
的代數式表示).
(2)若三種花卉共栽種![]() 株
株
①求![]() 與
與![]() 的值.
的值.
②若三種花卉的單價(都是整數)之和為![]() 元,全部栽種共需
元,全部栽種共需![]() 元,求種植面積最大的花卉總價.
元,求種植面積最大的花卉總價.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com