Question

【題目】如圖，OA、OB、OC都是⊙O的半徑，∠AOB=2∠BOC，

（1）求證：∠ACB=2∠BAC；

（2）若AC平分∠OAB，求∠AOC的度數．

Answer 1

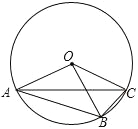
【答案】(1)證明詳見解析；(2)135°．

【解析】

試題分析：（1）根據圓周角定理可得∠BOC=2∠BAC，∠AOB=2∠ACB，再根據條件∠AOB=2∠BOC可得∠ACB=2∠BAC；

（2）設∠BAC=x°，則∠OAB=2∠BAC=2x°，再表示出∠AOB=2∠ACB=4∠BAC=4x°，再根據三角形內角和為180°可得方程4x+2x+2x=180，再解即可得x的值，進而可得答案．

試題解析：（1）在⊙O中，∵∠AOB=2∠ACB，∠BOC=2∠BAC，

∵∠AOB=2∠BOC．

∴∠ACB=2∠BAC；

（2）解：設∠BAC=x°．

∵AC平分∠OAB，

∴∠OAB=2∠BAC=2x°，

∵∠AOB=2∠ACB，∠ACB=2∠BAC，

∴∠AOB=2∠ACB=4∠BAC=4x°，

在△OAB中，

∠AOB+∠OAB+∠OBA=180°，

∴4x+2x+2x=180，

解得：x=22.5，

∴∠AOC=6x°=135°．